题目内容
12.先化简,再求值:[(a+b)2-(a+b)(a-b)-3b2]÷(-2b),其中|a-$\frac{1}{2}$|+(b+2)2=0.分析 直接利用乘法公式将原式化简,合并同类项,进而利用多项式除法运算法则化简,再将已知代入得出答案.
解答 解:[(a+b)2-(a+b)(a-b)-3b2]÷(-2b),
=[a2+2ab+b2-(a2-b2)-3b2]÷(-2b)
=(2ab-b2)÷(-2b)
=-a+$\frac{1}{2}$b
∵|a-$\frac{1}{2}$|+(b+2)2=0,
∴a=$\frac{1}{2}$,b=-2,
原式=-$\frac{1}{2}$+$\frac{1}{2}$×(-2)=-$\frac{3}{2}$.
点评 此题主要考查了整式的混合运算,正确掌握多项式乘除法运算法则是解题关键.

练习册系列答案
相关题目
2.若代数式y2+y-2的值为0,则代数式y3+4y2+y+2014的值为( )
| A. | 2014 | B. | 2015 | C. | 2020 | D. | 2025 |
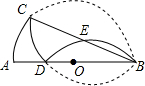 如图,AB是半圆O的直径,将半圆沿弦BC折叠,折叠后的圆弧与AB交于点D,再将弧BD沿AB对折后交弦BC于E,若E恰好是BC的中点,则BC:AB=$\frac{\sqrt{14}}{4}$.
如图,AB是半圆O的直径,将半圆沿弦BC折叠,折叠后的圆弧与AB交于点D,再将弧BD沿AB对折后交弦BC于E,若E恰好是BC的中点,则BC:AB=$\frac{\sqrt{14}}{4}$. 如图,数轴上表示1、$\sqrt{2}$的对应点分别为A、B,点B关于A的对称点为C,设点C表示的数为x,求(x-2)(2-x)的值.
如图,数轴上表示1、$\sqrt{2}$的对应点分别为A、B,点B关于A的对称点为C,设点C表示的数为x,求(x-2)(2-x)的值.