题目内容
4.计算:(1)3$\sqrt{48}$-9$\sqrt{\frac{1}{3}}$+3$\sqrt{12}$;
(2)(5+2$\sqrt{3}$)(2-2$\sqrt{3}$);
(3)($\frac{1}{\sqrt{5}}$+$\sqrt{20}$-3$\sqrt{5}$)×$\sqrt{10}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)利用多项式乘法公式展开,然后合并即可;
(3)先根据二次根式的乘除法则运算,然后化简后合并即可.
解答 解:(1)原式=12$\sqrt{3}$-3$\sqrt{3}$+6$\sqrt{3}$
=15$\sqrt{3}$;
(2)原式=10-10$\sqrt{3}$+4$\sqrt{3}$-12
=-2-6$\sqrt{3}$;
(3)原式=$\sqrt{2}$+10$\sqrt{2}$-15$\sqrt{2}$
=-4$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
14.下列能判定四边形是平行四边形的有( )
| A. | 一组对边相等,一组对角也相等 | |
| B. | 一组对边相等,一条对角线被另一条平分 | |
| C. | 一组对角相等,一条对角线被另一条平分 | |
| D. | 一组对角相等,过这组对角的顶点的对角线平分另一条对角线 |
16.“$\frac{16}{49}$的平方根是±$\frac{4}{7}$”用数学式表示为( )
| A. | $\sqrt{\frac{16}{49}}$=±$\frac{4}{7}$ | B. | $\sqrt{\frac{16}{49}}$=$\frac{4}{7}$ | C. | ±$\sqrt{\frac{16}{49}}$=±$\frac{4}{7}$ | D. | -$\sqrt{\frac{16}{49}}$=-$\frac{4}{7}$ |
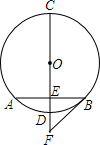 如图,CD是⊙O的直径,弦AB⊥CD于点E,且AB=2$\sqrt{2}$,DE=2-$\sqrt{2}$.
如图,CD是⊙O的直径,弦AB⊥CD于点E,且AB=2$\sqrt{2}$,DE=2-$\sqrt{2}$.
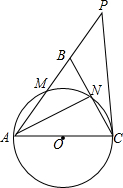 如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
 直线MN表示一条河流的河岸,在河流同旁有A、B两个村庄,现要在河边修建一个供水站给A、B供水.问:这个供水站建在什么地方,可以使铺设管道最短?请在图中找出表示供水站的点P.
直线MN表示一条河流的河岸,在河流同旁有A、B两个村庄,现要在河边修建一个供水站给A、B供水.问:这个供水站建在什么地方,可以使铺设管道最短?请在图中找出表示供水站的点P. 如图,已知l1∥l2,l3和直线l1,l2分别交于A、B两点,点P在直线AB.
如图,已知l1∥l2,l3和直线l1,l2分别交于A、B两点,点P在直线AB.