题目内容
19.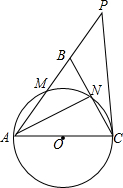 如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.(1)求证:直线CP是⊙O的切线;
(2)若BC=2$\sqrt{5}$,sin∠BCP=$\frac{\sqrt{5}}{5}$,求点B到AC的距离.
分析 (1)利用直径所对的圆周角为直角,2∠CAN=∠CAB,∠CAB=2∠BCP判断出∠ACP=90°即可;
(2)利用锐角三角函数,即勾股定理即可.
解答 (1)证明:∵∠ABC=∠ACB,
∴AB=AC,
∵AC为⊙O的直径,
∴∠ANC=90°,
∴∠CAN+∠ACN=90°,2∠BAN=2∠CAN=∠CAB,
∵∠CAB=2∠BCP,
∴∠BCP=∠CAN,
∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°,
∵点D在⊙O上,
∴直线CP是⊙O的切线;
(2)如图,作BF⊥AC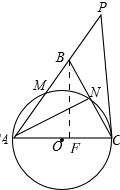
∵AB=AC,∠ANC=90°,
∴CN=$\frac{1}{2}$CB=$\sqrt{5}$,
∵∠BCP=∠CAN,sin∠BCP=$\frac{\sqrt{5}}{5}$,
∴sin∠CAN=$\frac{\sqrt{5}}{5}$,
∴$\frac{CN}{AC}=\frac{\sqrt{5}}{5}$,
∴AC=5,
∴AB=AC=5,
设AF=x,则CF=5-x,
在Rt△ABF中,BF2=AB2-AF2=25-x2,
在Rt△CBF中,BF2=BC2-CF2=2O-(5-x)2,
∴25-x2=2O-(5-x)2,
∴x=3,
∴BF2=25-32=16,
∴BF=4,
即点B到AC的距离为4.
点评 此题是切线的判定,主要考查了切线的判定定理,勾股定理得应用,构造出直角三角形Rt△ABF和Rt△CBF是解本题的关键.

练习册系列答案
相关题目
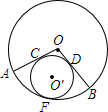 如图,在⊙O中,圆心角∠AOB=120°,⊙O′与OA、OB相切于点C、D,与$\widehat{AB}$相切于F,求$\widehat{AB}$的长与⊙O′的周长的比.
如图,在⊙O中,圆心角∠AOB=120°,⊙O′与OA、OB相切于点C、D,与$\widehat{AB}$相切于F,求$\widehat{AB}$的长与⊙O′的周长的比. 如图,已知直线l1,l2,l3被直线l所截,∠1=72°,∠2=108°,∠3=72°,试说明l1∥l2∥l3.
如图,已知直线l1,l2,l3被直线l所截,∠1=72°,∠2=108°,∠3=72°,试说明l1∥l2∥l3. 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点A,再在河岸的这一边选取点B和点C,使AB⊥BC,然后再选取点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=160m,DC=80m,EC=50m,求A、B间的大致距离.
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点A,再在河岸的这一边选取点B和点C,使AB⊥BC,然后再选取点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=160m,DC=80m,EC=50m,求A、B间的大致距离.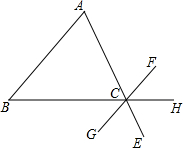 如图所示,请写出一个条件∠B=∠BCG,使AB∥FG.
如图所示,请写出一个条件∠B=∠BCG,使AB∥FG.