题目内容
14. 如图,已知l1∥l2,l3和直线l1,l2分别交于A、B两点,点P在直线AB.
如图,已知l1∥l2,l3和直线l1,l2分别交于A、B两点,点P在直线AB.(1)如过点P在A、B两点之间运动,试探究∠1、∠2、∠3之间的关系,并证明.
(2)如果点P在A、B两点外侧运动(不与A、B重合),试探究∠1、∠2、∠3之间的关系,并证明.
分析 (1)过P作PE∥AC,再由l1∥l2,可证明出PE∥BD,根据平行线的性质可得∠EPD=∠2,∠EPC=∠1,进而可得∠1+∠2=∠3;
(2)利用P点l1上方或在l2下方分析,证法与(1)相同.
解答 解:(1)∠1+∠2=∠3,
如图1所示:过P作PE∥AC,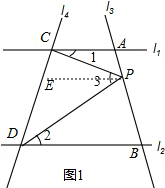
∵l1∥l2,
∴PE∥BD,
∴∠EPD=∠2,
∵PE∥AC,
∴∠EPC=∠1,
∴∠1+∠2=∠3;
(2)∠1-∠2=∠3或∠2-∠1=∠3
理由:如图2所示: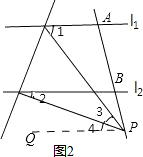
当点P在下侧时,过点P作l1的平行线PQ,
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠2=∠4,∠1=∠3+∠4,(两直线平行,内错角相等)
∴∠1-∠2=∠3;
当点P在上侧时,同理可得:∠2-∠1=∠3.
点评 此题主要考查了平行线的性质,关键是掌握两直线平行,内错角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
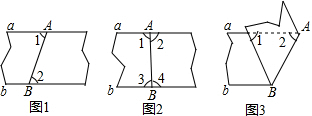
2.三名同学分别沿AB折叠纸条,哪名间学的折法一定能判定两条边线a,b互相平行?为什么?
小明:如图1,展开后测得∠1=∠2
小红:如图2,展开后测得∠1=∠2且∠3=∠4.
小刚:如图3,测得∠1=∠2.
小明:如图1,展开后测得∠1=∠2
小红:如图2,展开后测得∠1=∠2且∠3=∠4.
小刚:如图3,测得∠1=∠2.

6.如果?ABCD的周长为40cm,△ABC的周长为25cm,则对角线AC的长是( )
| A. | 5cm | B. | 15cm | C. | 6cm | D. | 16cm |
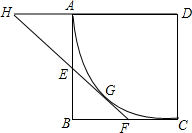 如图,正方形ABCD的边长为6,以D为圆心,DA为半径作⊙D,E在AB上,EF切⊙D于G,交BC于F.
如图,正方形ABCD的边长为6,以D为圆心,DA为半径作⊙D,E在AB上,EF切⊙D于G,交BC于F.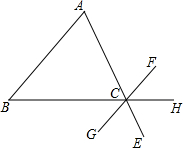 如图所示,请写出一个条件∠B=∠BCG,使AB∥FG.
如图所示,请写出一个条件∠B=∠BCG,使AB∥FG.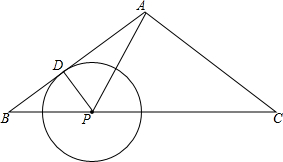 如图,在△ABC中,AB=AC=10,BC=16,点P为BC边上的一个动点,以P为圆心的⊙P与边AB相切于点D.在点P移动的过程中,△APC如果成为等腰三角形,求⊙P的半径.
如图,在△ABC中,AB=AC=10,BC=16,点P为BC边上的一个动点,以P为圆心的⊙P与边AB相切于点D.在点P移动的过程中,△APC如果成为等腰三角形,求⊙P的半径.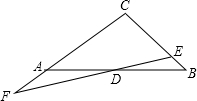 如图,△ABC中,D为边AB的中点,E为边BC上一点,ED延长线交CA延长线于点F,以下结论正确的有②④.
如图,△ABC中,D为边AB的中点,E为边BC上一点,ED延长线交CA延长线于点F,以下结论正确的有②④.