题目内容
15.等腰三角形的两个内角的度数之比为a:b(a<b),若这个三角形是钝角三角形,则b:a的取值范围是$\frac{b}{a}$>2.分析 设等腰三角形的两个内角的度数分别是ax、bx.由该三角形是钝角三角形得到该等腰三角形的三个内角的度数分别是ax、ax、bx.依据钝角三角形的定义来求b:a的取值范围.
解答 解:设等腰三角形的两个内角的度数分别是ax、bx.
∵a<b,且该等腰三角形是钝角三角形,
∴该等腰三角形的三个内角的度数分别是ax、ax、bx.
∴2ax<90°,即ax<45°,
bx>90°,
∴ax:bx<$\frac{1}{2}$,即b:a的取值范围是:$\frac{b}{a}$>2.
故答案是:$\frac{b}{a}$>2.
点评 本题考查了等腰三角形的性质.此题有限制性条件a<b、这个三角形是钝角三角形可以判定b是顶角.

练习册系列答案
相关题目
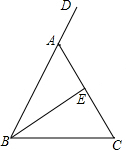 如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.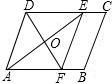 如图,在?ABCD中,AE是∠DAB的平分线,EF∥AD交B于点F,连接DF交AE于点O,
如图,在?ABCD中,AE是∠DAB的平分线,EF∥AD交B于点F,连接DF交AE于点O,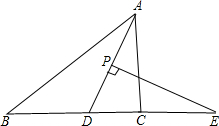 在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E(∠ABC、∠ACB的大小不确定).
在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E(∠ABC、∠ACB的大小不确定).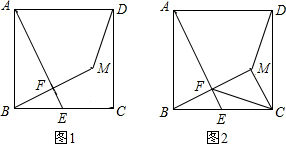
 平面直角坐标系中,标出并顺次连结A(-2,1),B(-2,-1),C(2,1),D(2,3)各点,你会得到一个什么图形?试求出该图形的面积.
平面直角坐标系中,标出并顺次连结A(-2,1),B(-2,-1),C(2,1),D(2,3)各点,你会得到一个什么图形?试求出该图形的面积. 如图,正方形ABCD的对角线交于点O,点F是BC的中点.
如图,正方形ABCD的对角线交于点O,点F是BC的中点.