题目内容
14.设x1,x2是关于x的方程x2-(m-1)x-m=0(m≠0)的两个根,且满足$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$+$\frac{2}{3}$=0,求m的值.分析 根据根与系数的关系得到x1+x2=m-1,x1x2=-m,再变形$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$+$\frac{2}{3}$=0得到$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$+$\frac{2}{3}$=0,则$\frac{m-1}{-m}$+$\frac{2}{3}$=0,解得m=3,然后根据判别式的意义确定m的值.
解答 解:根据题意得x1+x2=m-1,x1x2=-m,
∵$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$+$\frac{2}{3}$=0,
∴$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$+$\frac{2}{3}$=0,
∴$\frac{m-1}{-m}$+$\frac{2}{3}$=0,解得m=3,
而m=3时,△>0,
∴m的值为3.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
2.不等式组$\left\{\begin{array}{l}{x-3<2}\\{x≥-1}\end{array}\right.$的解集是( )
| A. | x≥-1 | B. | x<5 | C. | -1≤x<5 | D. | x≤-1或x>5 |
19.在一次学生田径运动会上,参加跳高的15名运动员的成绩如下表所示:
那么这些运动员跳高成绩的众数是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 1 | 3 | 5 | 3 | 2 |
| A. | 3 | B. | 5 | C. | 1.65 | D. | 1.70 |
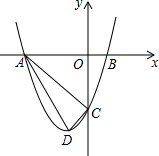 二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C(0,-3m)(其中m>0),顶点为D.
二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C(0,-3m)(其中m>0),顶点为D.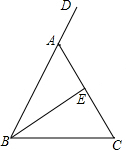 如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.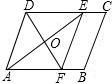 如图,在?ABCD中,AE是∠DAB的平分线,EF∥AD交B于点F,连接DF交AE于点O,
如图,在?ABCD中,AE是∠DAB的平分线,EF∥AD交B于点F,连接DF交AE于点O,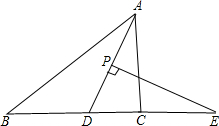 在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E(∠ABC、∠ACB的大小不确定).
在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E(∠ABC、∠ACB的大小不确定). 如图,正方形ABCD的对角线交于点O,点F是BC的中点.
如图,正方形ABCD的对角线交于点O,点F是BC的中点.