题目内容
19.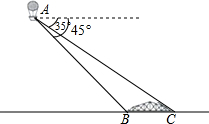 小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.(结果保留整数)
小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.(结果保留整数)(参考数据:sin35°≈$\frac{7}{12}$,cos35°≈$\frac{5}{6}$,tan35°≈$\frac{7}{10}$)
分析 作AD⊥BC交CB的延长线于D,设AD为x,表示出DB和DC,根据正切的概念求出x的值即可.
解答 解:作AD⊥BC交CB的延长线于D,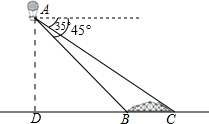 设AD为x,
设AD为x,
由题意得,∠ABD=45°,∠ACD=35°,
在Rt△ADB中,∠ABD=45°,
∴DB=x,
在Rt△ADC中,∠ACD=35°,
∴tan∠ACD=$\frac{AD}{CD}$,
∴$\frac{x}{x+100}$=$\frac{7}{10}$,
解得,x≈233m.
点评 本题考查的是解直角三角形的应用,理解仰角和俯角的概念、掌握锐角三角函数的概念是解题的关键,解答时,注意正确作出辅助线构造直角三角形.

练习册系列答案
相关题目
9.一个多边形的内角和为1080°,则它的边数为( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
14. 如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
 如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )| A. | x<-2或x>2 | B. | x<-2或0<x<2 | C. | -2<x<0或0<x<2 | D. | -2<x<0或x>2 |
8.一个等腰三角形的两条边长分别是方程x2-7x+10=0的两根,则该等腰三角形的周长是( )
| A. | 12 | B. | 9 | C. | 13 | D. | 12或9 |
12.下列命题中,是假命题的是( )
| A. | 互余两角的和是90° | B. | 全等三角形的面积相等 | ||
| C. | 等边三角形是中心对称图形 | D. | 两直线平行,同旁内角互补 |
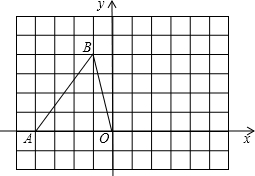 如图,在平面直角坐标系中,点A、B的坐标分别为A(-4,0),B(-1,4),将△AOB绕点O顺时针旋转90°
如图,在平面直角坐标系中,点A、B的坐标分别为A(-4,0),B(-1,4),将△AOB绕点O顺时针旋转90°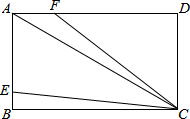 如图,AC是矩形ABCD的对角线,AB=2,BC=2$\sqrt{3}$,点E,F分别是线段AB,AD上的点,连接CE,CF.当∠BCE=∠ACF,且CE=CF时,AE+AF=$\frac{4\sqrt{3}}{3}$.
如图,AC是矩形ABCD的对角线,AB=2,BC=2$\sqrt{3}$,点E,F分别是线段AB,AD上的点,连接CE,CF.当∠BCE=∠ACF,且CE=CF时,AE+AF=$\frac{4\sqrt{3}}{3}$.