题目内容
10.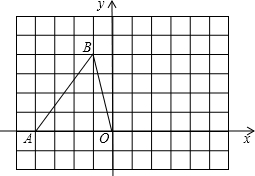 如图,在平面直角坐标系中,点A、B的坐标分别为A(-4,0),B(-1,4),将△AOB绕点O顺时针旋转90°
如图,在平面直角坐标系中,点A、B的坐标分别为A(-4,0),B(-1,4),将△AOB绕点O顺时针旋转90°(1)画出旋转后的△A′OB′;
(2)写出点B关于原点O的对称点的坐标;
(3)求出点B到点B′所经过的路径长;
(4)用直尺和圆规作出△A′OB′的外接圆(保留作图痕迹,不写作法).
分析 (1)根据网格结构找出点A、B绕点O顺时针旋转90°后的对应点A′、B′的位置,然后顺次连接即可;
(2)根据关于原点对称的点横坐标与纵坐标都是互为相反数即可求解;
(3)根据弧长公式即可得出结论;
(4)根据外接圆的圆心到三角形三个顶点的距离相等,知它是三角形三边的垂直平分线的交点,则作其两边的垂直平分线,以交点为圆心,交点到其中一个顶点的距离为半径的圆是三角形的外接圆.
解答 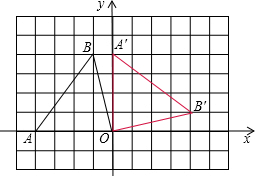 解:(1)如图所示:
解:(1)如图所示:
(2)点B(-1,4)关于原点O的对称点的坐标为(1,-4);
(3)∵OB=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,∠BOB′=90°,
∴点B到点B′所经过的路径长为:$\frac{90π×\sqrt{17}}{180}$=$\frac{\sqrt{17}}{2}$π;
(4)如图所示: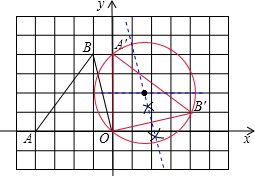
点评 此题考查了作图-旋转变换,关于原点对称的点的坐标,旋转的性质,弧长的计算,三角形外接圆的作法,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
2. 如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为( )
如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为( )
 如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为( )
如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为( )| A. | 13 | B. | $\frac{15}{2}$ | C. | $\frac{27}{2}$ | D. | 12 |
 如图,已知AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E,连接AE、DF.试说明:
如图,已知AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E,连接AE、DF.试说明: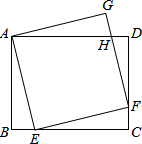 如图,在矩形ABCD中,AB=4,BC=5.点E在边BC上,以AE为边作正方形AEFG,顶点F恰好在边CD上,FG与AD交于点H.则DH的长为$\frac{3}{4}$.
如图,在矩形ABCD中,AB=4,BC=5.点E在边BC上,以AE为边作正方形AEFG,顶点F恰好在边CD上,FG与AD交于点H.则DH的长为$\frac{3}{4}$.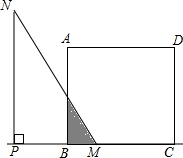 如图,正方形ABCD的边长为2cm,△PMN是直角一块三角板(∠N=30°),PM>2cm,PM与BC均在直线l上,开始时M点与B点重合,将三角板向右平行移动,直至M点与C点重合为止.设BM=xcm,三角板与正方形重叠部分的面积外ycm2.
如图,正方形ABCD的边长为2cm,△PMN是直角一块三角板(∠N=30°),PM>2cm,PM与BC均在直线l上,开始时M点与B点重合,将三角板向右平行移动,直至M点与C点重合为止.设BM=xcm,三角板与正方形重叠部分的面积外ycm2.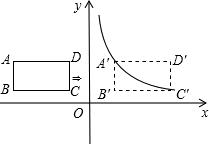 如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2.
如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2.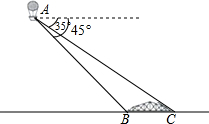 小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.(结果保留整数)
小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.(结果保留整数)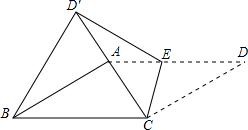 如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为D′,连接D′B,若△D′BC为等边三角形,则DE=2$\sqrt{3}$-2或$\sqrt{3}$+1.
如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为D′,连接D′B,若△D′BC为等边三角形,则DE=2$\sqrt{3}$-2或$\sqrt{3}$+1.