题目内容
14．
如图，正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A，B两点，其中点A的横坐标为2，当y1＞y2时，x的取值范围是（ ）| A． | x＜-2或x＞2 | B． | x＜-2或0＜x＜2 | C． | -2＜x＜0或0＜x＜2 | D． | -2＜x＜0或x＞2 |
分析 先根据反比例函数与正比例函数的性质求出B点坐标，再由函数图象即可得出结论．
解答 解：∵反比例函数与正比例函数的图象均关于原点对称，
∴A、B两点关于原点对称，
∵点A的横坐标为2，
∴点B的横坐标为-2，
∵由函数图象可知，当-2＜x＜0或x＞2时函数y1=k1x的图象在y2=$\frac{{k}_{2}}{x}$的上方，
∴当y1＞y2时，x的取值范围是-2＜x＜0或x＞2．
故选D．
点评 本题考查的是反比例函数与一次函数的交点问题，能根据数形结合求出y1＞y2时x的取值范围是解答此题的关键．
练习册系列答案
全能测控期末小状元系列答案
相关题目
2．
如图，在△ABC中，AB=AC，BC=24，tanC=2，如果将△ABC沿直线l翻折后，点B落在边AC的中点E处，直线l与边BC交于点D，那么BD的长为（ ）
如图，在△ABC中，AB=AC，BC=24，tanC=2，如果将△ABC沿直线l翻折后，点B落在边AC的中点E处，直线l与边BC交于点D，那么BD的长为（ ）| A． | 13 | B． | $\frac{15}{2}$ | C． | $\frac{27}{2}$ | D． | 12 |
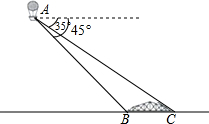小明在热气球A上看到正前方横跨河流两岸的大桥BC，并测得B，C两点的俯角分别为45°，35°．已知大桥BC与地面在同一水平面上，其长度为100m，请求出热气球离地面的高度．（结果保留整数）