题目内容
3.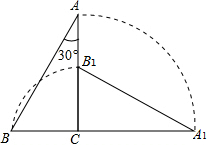 如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )| A. | π | B. | $\frac{11}{12}$$π+\frac{\sqrt{3}}{4}$ | C. | $π+\frac{\sqrt{3}}{4}$ | D. | $\frac{3π}{4}$$+\frac{\sqrt{3}}{2}$ |
分析 根据直角三角形的性质求出BC、AC的长度,设点B扫过的路线与AB的交点为D,连接CD,可以证明△BCD是等边三角形,然后求出点D是AB的中点,所以△ACD的面积等于△ABC的面积的一半,然后根据△ABC扫过的面积=S扇形ACA1+S扇形BCD+S△ACD,然后根据扇形的面积公式与三角形的面积公式列式计算即可得解.
解答 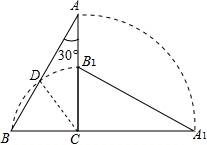 解:在△ABC中,∠ACB=90°,∠BAC=30°,AB=2,
解:在△ABC中,∠ACB=90°,∠BAC=30°,AB=2,
∴BC=$\frac{1}{2}$AB=1,∠B=90°-∠BAC=60°,
∴AC=$\sqrt{{AB}^{2}-{BC}^{2}}$=$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$×BC×AC=$\frac{\sqrt{3}}{2}$,
设点B扫过的路线与AB的交点为D,连接CD,
∵BC=DC,
∴△BCD是等边三角形,
∴BD=CD=1,
∴点D是AB的中点,
∴S△ACD=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$,
∴△ABC扫过的面积=S扇形ACA1+S扇形BCD+S△ACD,
=$\frac{90}{360}$×π×($\sqrt{3}$)2+$\frac{60}{360}$×π×12+$\frac{\sqrt{3}}{4}$,
=$\frac{3}{4}$π+$\frac{1}{6}$π+$\frac{\sqrt{3}}{4}$,
=$\frac{11}{12}$π+$\frac{\sqrt{3}}{4}$.
故选B.
点评 此题考查了扇形面积的计算及旋转的性质、直角三角形的性质以及等边三角形的性质,注意掌握旋转前后图形的对应关系,利用数形结合思想把扫过的面积分成两个扇形的面积与一个三角形面积是解题的关键,也是本题的难点.

| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
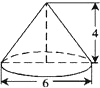 如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是( )
如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是( )| A. | 12π | B. | 15π | C. | 20π | D. | 30π |
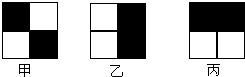
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 三个都一样 |
| A. | b2+c2=a2 | B. | c2=3b2 | C. | 3a2=2c2 | D. | c2=2b2 |
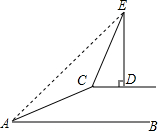 如图,某河大堤上有一棵树ED,ED⊥CD,并且CD与水平地面AB平行,小明在A处测得树顶E的仰角为45°,然后沿着坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,求树ED的高度.(精确到1米)
如图,某河大堤上有一棵树ED,ED⊥CD,并且CD与水平地面AB平行,小明在A处测得树顶E的仰角为45°,然后沿着坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,求树ED的高度.(精确到1米)