题目内容
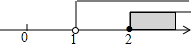
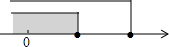
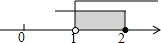
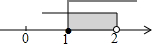
15．如图，有甲、乙、丙三种游戏盘，游戏规则如下：向游戏盘中掷小球（小球不会跑到盘子外面也不会停在黑白分界线上），小球停在黑色区域为赢．如果参加这次游戏，你认为选用哪个游戏盘赢的可能性大些？答（ ）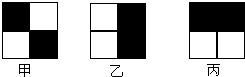
| A． | 甲 | B． | 乙 | C． | 丙 | D． | 三个都一样 |
分析 根据概率公式分别求出这3个小球停在黑色区域的概率，再进行比较即可．
解答 解：甲小球停在黑色区域的概率是：$\frac{2}{4}$=$\frac{1}{2}$；
乙小球停在黑色区域的概率是：$\frac{2}{4}$=$\frac{1}{2}$；
丙小球停在黑色区域的概率是：$\frac{2}{4}$=$\frac{1}{2}$；
则三个游戏盘赢的可能都一样；
故选D．
点评 本题考查的是可能性的大小，根据题意得出三种情况的概率是解答此题的关键．
练习册系列答案
相关题目
3．
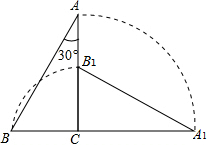如图，把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C，则在旋转过程中这个三角板扫过的图形的面积是（ ）
如图，把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C，则在旋转过程中这个三角板扫过的图形的面积是（ ）| A． | π | B． | $\frac{11}{12}$$π+\frac{\sqrt{3}}{4}$ | C． | $π+\frac{\sqrt{3}}{4}$ | D． | $\frac{3π}{4}$$+\frac{\sqrt{3}}{2}$ |
10．一个袋中装有标记数分别为-2，1，6的三张卡片（除标记外完全相同），先从袋中随机取出一张卡片，把卡片上标记数作为点A的横坐标，放回后再从袋中随机取出一张卡片，把标记数作为点A的纵坐标，则点A在第一象限的概率是（ ）
| A． | $\frac{2}{9}$ | B． | $\frac{1}{3}$ | C． | $\frac{4}{9}$ | D． | $\frac{5}{9}$ |
4．下列运算正确的是（ ）
| A． | （2x2）3=6x6 | B． | 3a+2b=5ab | C． | -a5•a5=-a10 | D． | （a+b）2=a2+b2 |