题目内容
13.△ABC中,∠A:∠B:∠C=1:1:2,a,b,c分别为∠A,∠B,∠C的对边,则有( )| A. | b2+c2=a2 | B. | c2=3b2 | C. | 3a2=2c2 | D. | c2=2b2 |
分析 根据已知条件和三角形的内角和即可得到△ABC是等腰直角三角形,于是得到结论.
解答 解:∵∠A:∠B:∠C=1:1:2,
∴设∠A=α,∠B=α,∠C=2α,
∵∠A+∠B+∠C=180°,
∴α+α+2α=180°,
∴α=45°,2α=90°,
∴∠A=∠B=45°,∠C=90°,
∴a=b,
∴a2+b2=c2,
即:c2=2b2,
故选:D.
点评 本题考查了等腰直角三角形的性质和判定,熟练掌握其性质是解题的关键.

练习册系列答案
相关题目
3.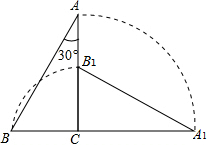 如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
 如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )| A. | π | B. | $\frac{11}{12}$$π+\frac{\sqrt{3}}{4}$ | C. | $π+\frac{\sqrt{3}}{4}$ | D. | $\frac{3π}{4}$$+\frac{\sqrt{3}}{2}$ |
4.下列运算正确的是( )
| A. | (2x2)3=6x6 | B. | 3a+2b=5ab | C. | -a5•a5=-a10 | D. | (a+b)2=a2+b2 |
3.若(x-6)(x+p)=x2+2mx+36,则p、m的值分别是( )
| A. | -6,-6 | B. | -6,-12 | C. | 6,0 | D. | 6,6 |