题目内容
12.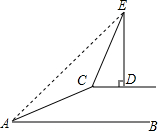 如图,某河大堤上有一棵树ED,ED⊥CD,并且CD与水平地面AB平行,小明在A处测得树顶E的仰角为45°,然后沿着坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,求树ED的高度.(精确到1米)
如图,某河大堤上有一棵树ED,ED⊥CD,并且CD与水平地面AB平行,小明在A处测得树顶E的仰角为45°,然后沿着坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,求树ED的高度.(精确到1米)(参考数据:sin76°≈0.97,cos76°=0.24,tan76°≈4.01,$\sqrt{5}$=2.236)
分析 过点D作DF⊥AB于点F,过点C作CG⊥AB于点G,根据坡度比求出AG和CG,设CD=x米,再根据正切值表示出ED,根据∠EAF=45°,求出x的值,再把x的值代入即可得出答案.
解答 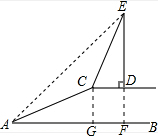 解:过点D作DF⊥AB于点F,过点C作CG⊥AB于点G,
解:过点D作DF⊥AB于点F,过点C作CG⊥AB于点G,
∵坡度为1:2,
∴CG:AG=1:2,
∴AG:AC=2:$\sqrt{5}$,
∵AC=20米,
∴AG=8$\sqrt{5}$米,CG=4$\sqrt{5}$米,
设CD=x米,
∵∠ECD=76°,
∴ED=CD•tan76°=4.01x(米),
∵ED⊥CD,CD∥AB,
∴点E,D,F共线,
∵∠EAF=45°,
∴tan∠EAF=tan45°=$\frac{EF}{AF}$=1,
∴$\frac{4.01x+4\sqrt{5}}{8\sqrt{5}+x}$=1,
∴x≈2.99米,
∴ED=4.01×2.99≈12(米).
答:树ED的高度是12米.
点评 此题考查了解直角三角形、勾股定理、锐角三角函数以及坡角与坡角等知识.解题的关键是做出辅助线,构造直角三角形.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
3.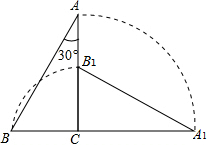 如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
 如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )| A. | π | B. | $\frac{11}{12}$$π+\frac{\sqrt{3}}{4}$ | C. | $π+\frac{\sqrt{3}}{4}$ | D. | $\frac{3π}{4}$$+\frac{\sqrt{3}}{2}$ |
4.下列运算正确的是( )
| A. | (2x2)3=6x6 | B. | 3a+2b=5ab | C. | -a5•a5=-a10 | D. | (a+b)2=a2+b2 |