题目内容
18.若点(-3,y1)(-1,y2)(1,y3)在反比例函数y=$\frac{-{k}^{2}+2k-3}{x}$的图象上,则y1、y2、y3的关系是y3<y1<y2(按从小到大排列).分析 利用配方法和非负数的性质可判断-k2+2k-3<0,易得y3<0,y1>0,y2>0,然后根据反比例函数的性质可判断y1<y2,从而得到y1、y2、y3的大小关系.
解答 解:-k2+2k-3=-(k-1)2-2<0,
∵(-3,y1)(-1,y2)(1,y3)在反比例函数y=$\frac{-{k}^{2}+2k-3}{x}$的图象上,
∴y3<y1<y2.
故答案为y3<y1<y2.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.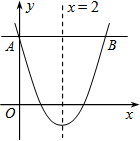 如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
 如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )| A. | (2,3) | B. | (3,2) | C. | (3,4) | D. | (4,3) |
13.在实数范围内因式分解x3-2x的结果是( )
| A. | x(x2-2) | B. | x(x-1)2 | C. | x(x-$\sqrt{2}$)(x$+\sqrt{2}$) | D. | x(x-$\sqrt{2}$)2 |
3.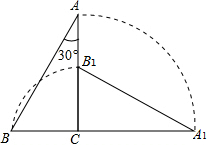 如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
 如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )| A. | π | B. | $\frac{11}{12}$$π+\frac{\sqrt{3}}{4}$ | C. | $π+\frac{\sqrt{3}}{4}$ | D. | $\frac{3π}{4}$$+\frac{\sqrt{3}}{2}$ |
10.一个袋中装有标记数分别为-2,1,6的三张卡片(除标记外完全相同),先从袋中随机取出一张卡片,把卡片上标记数作为点A的横坐标,放回后再从袋中随机取出一张卡片,把标记数作为点A的纵坐标,则点A在第一象限的概率是( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |