题目内容
16.已知⊙O1与⊙O2的半径分别为2和4,圆心距O1O2=6,则两圆的位置关系是( )| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
分析 根据两圆外切p=R+r,可得答案.
解答 解:由⊙O1与⊙O2的半径分别为2和4,圆心距O1O2=6,得
2+4=6,
即O1O2=r+R,
故选:B.
点评 本题考查了圆与圆的位置关系,外离,则P>R+r;外切,则P=R+r;相交,则R-r<P<R+r;内切,则P=R-r;内含,则P<R-r,(P表示圆心距,R,r分别表示两圆的半径).

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
6.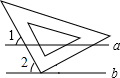 如图,直线a∥b,三角板的直角顶点放在直线b上,两直角边与直线a相交,如果∠1=55°,那么∠2的度数为( )
如图,直线a∥b,三角板的直角顶点放在直线b上,两直角边与直线a相交,如果∠1=55°,那么∠2的度数为( )
 如图,直线a∥b,三角板的直角顶点放在直线b上,两直角边与直线a相交,如果∠1=55°,那么∠2的度数为( )
如图,直线a∥b,三角板的直角顶点放在直线b上,两直角边与直线a相交,如果∠1=55°,那么∠2的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
7.下列各式中,计算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{12}-\sqrt{3}=3$ | C. | $\sqrt{2}×\sqrt{3}=\sqrt{5}$ | D. | $\sqrt{12}÷\sqrt{3}=2$ |
11.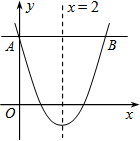 如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
 如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )| A. | (2,3) | B. | (3,2) | C. | (3,4) | D. | (4,3) |
3.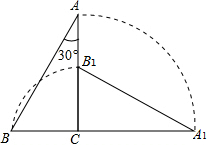 如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
 如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )| A. | π | B. | $\frac{11}{12}$$π+\frac{\sqrt{3}}{4}$ | C. | $π+\frac{\sqrt{3}}{4}$ | D. | $\frac{3π}{4}$$+\frac{\sqrt{3}}{2}$ |
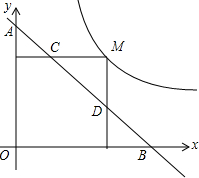 如图,反比例函数$y=\frac{k}{x}$经过点(1,$\sqrt{3}$),则k=$\sqrt{3}$;若点M为该曲线上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为2$\sqrt{3}$.
如图,反比例函数$y=\frac{k}{x}$经过点(1,$\sqrt{3}$),则k=$\sqrt{3}$;若点M为该曲线上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为2$\sqrt{3}$.