题目内容
3.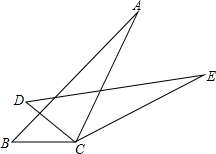 如图所示,∠B=∠D,BC=DC,要判定△ABC≌△EDC,当添加条件∠ACB=∠ECD时,可根据”ASA“判定;当添加条件∠A=∠E时.可根据“AAS”判定;当添加条件AB=ED时,可根据“SAS”判定.
如图所示,∠B=∠D,BC=DC,要判定△ABC≌△EDC,当添加条件∠ACB=∠ECD时,可根据”ASA“判定;当添加条件∠A=∠E时.可根据“AAS”判定;当添加条件AB=ED时,可根据“SAS”判定.
分析 由于BC是∠B与∠ACB的夹边,DC是∠D与∠ECD的夹边,∠B=∠D,BC=DC,要通过“ASA”判定△ABC≌△EDC,只需∠ACB=∠ECD即可;由于BC是∠A的对边,DC是∠E的对边,∠B=∠D,BC=DC,要通过“AAS”判定△ABC≌△EDC,只需∠A=∠E即可;由于∠B是BC与AB的夹角,∠D是DC与DE的夹角,∠B=∠D,BC=DC,要通过“SAS”判定△ABC≌△EDC,只需AB=ED即可.
解答 解:当∠ACB=∠ECD时,
在△ABC和△EDC中,
$\left\{\begin{array}{l}{∠B=∠D}\\{BC=DC}\\{∠ACB=∠ECD}\end{array}\right.$,
∴△ABC≌△EDC(ASA).
当∠A=∠E时,
在△ABC和△EDC中,
$\left\{\begin{array}{l}{∠A=∠E}\\{∠B=∠D}\\{BC=DC}\end{array}\right.$,
∴△ABC≌△EDC(AAS).
当AB=ED时,
在△ABC和△EDC中,
$\left\{\begin{array}{l}{AB=ED}\\{∠B=∠D}\\{BC=DC}\end{array}\right.$,
∴△ABC≌△EDC(SAS).
故答案分别为∠ACB=∠ECD,∠A=∠E,AB=ED.
点评 本题主要考查了两个三角形全等的判定的简单运用,两个三角形全等通常有四种判定方法:SAS、ASA、AAS、SSS;两个直角三角形全等除了以上四种判定方法以外,还有HL.

练习册系列答案
相关题目
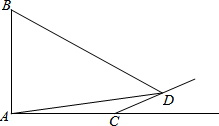 如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:$\sqrt{3}$,求旗杆AB的高度($\sqrt{3}≈1.7$,结果精确到个位).
如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:$\sqrt{3}$,求旗杆AB的高度($\sqrt{3}≈1.7$,结果精确到个位). 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图形在第一象限相交于点A(1,-k+4).
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图形在第一象限相交于点A(1,-k+4).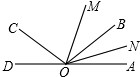 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=50°,试求∠AOC与∠AOB的度数.
如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=50°,试求∠AOC与∠AOB的度数.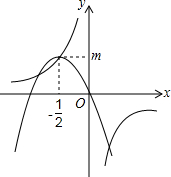 如图,反比例函数y=$\frac{1}{ax}$(a≠0)的图象经过二次函数y=ax2+bx图象的顶点(-$\frac{1}{2}$,m)(m>0),则m=$\frac{\sqrt{2}}{2}$.
如图,反比例函数y=$\frac{1}{ax}$(a≠0)的图象经过二次函数y=ax2+bx图象的顶点(-$\frac{1}{2}$,m)(m>0),则m=$\frac{\sqrt{2}}{2}$.