题目内容
15．
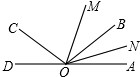如图，已知O为AD上一点，∠AOC与∠AOB互补，OM，ON分别为∠AOC，∠AOB的平分线，若∠MON=50°，试求∠AOC与∠AOB的度数．
分析 解此类题目关键在于：结合图形，根据余角、补角的定义，有时还需考虑角平分线的性质，分析并找到角与角之间的关系，再进行计算得出答案．
解答 解：设∠AOB=x°，因为∠AOC与∠AOB互补，则∠AOC=180°-x°．
由题意，得$\frac{180-x}{2}$-$\frac{x}{2}$=50．
∴180-x-x=100，
∴-2x=-80，
解得x=40
故∠AOB=40°，∠AOC=140°．
点评 本题结合图形考查余角、补角的定义；涉及了角平分线的性质，及角的运算．在图形中，找补角、余角关系时，除了借助图形外，还需考虑等量关系即有没有相等的角．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
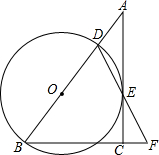在Rt△ABC中，∠ACB=90°，D是AB边上的一点，以BD为直径作⊙O．与AC相切于点E，连结DE并延长与BC的延长线交于点F．
如图，AB=6，将以AB为直径的半圆再绕点B顺时针旋转45°，点A旋转到A′的位置，则图中阴影部分的面积为$\frac{9}{2}$π．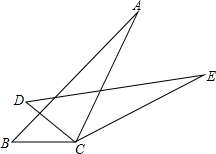
如图所示，∠B=∠D，BC=DC，要判定△ABC≌△EDC，当添加条件∠ACB=∠ECD时，可根据”ASA“判定；当添加条件∠A=∠E时．可根据“AAS”判定；当添加条件AB=ED时，可根据“SAS”判定．
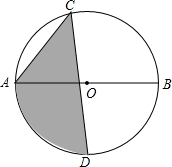如图，⊙O的直径AB为10，弦AC为6，△ACB的平分线交⊙O于点D，则图中阴影部分的面积为$\frac{17}{2}$+$\frac{25π}{4}$．
7．
如图，CD为△ABC的中线，且CD⊥AC，O为BC边上一点，以O为圆心，0C为长半径作⊙O，若⊙O与AB恰好相切于点D，则tanB=（ ）
如图，CD为△ABC的中线，且CD⊥AC，O为BC边上一点，以O为圆心，0C为长半径作⊙O，若⊙O与AB恰好相切于点D，则tanB=（ ）| A． | $\frac{1}{3}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{3}{8}$ | D． | $\frac{1}{2}$ |
．分别以B、D为圆心，AB为半径画弧，两弧分别交对角线BD于点E、F，则图中阴影部分的面积为__________.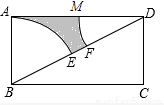
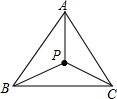如图，点P是正△ABC内一点．