题目内容
11. 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图形在第一象限相交于点A(1,-k+4).
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图形在第一象限相交于点A(1,-k+4).(1)试确定这两函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△AOB的面积;
(3)根据图象直接写出反比例函数值大于一次函数值的x的取值范围.
分析 (1)根据反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图形在第一象限相交于点A(1,-k+4),可以求得k的值,从而可以求得点A的坐标,从而可以求出一次函数y=x+b中b的值,本题得以解决;
(2)将第一问中求得的两个解析式联立方程组可以求得点B的坐标,进而可以求得△AOB的面积;
(3)根据函数图象可以解答本题.
解答 解;(1)∵反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图形在第一象限相交于点A(1,-k+4),
∴$-k+4=\frac{k}{1}$,
解得,k=2,
∴点A(1,2),
∴2=1+b,得b=1,
即这两个函数的表达式分别是:$y=\frac{2}{x}$,y=x+1;
(2)$\left\{\begin{array}{l}{y=\frac{2}{x}}\\{y=x+1}\end{array}\right.$
解得,$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,
即这两个函数图象的另一个交点B的坐标是(-2,-1);
将y=0代入y=x+1,得x=-1,
∴OC=|-1|=1,
∴S△AOB=S△AOC+S△BOC=$\frac{1×2}{2}+\frac{1×1}{2}=\frac{3}{2}$,
即△AOB的面积是$\frac{3}{2}$;
(3)根据图象可得反比例函数值大于一次函数值的x的取值范围是x<-2或0<x<1.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

 阅读快车系列答案
阅读快车系列答案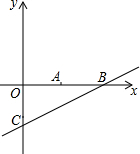 在平面直角坐标系xOy中,点A、点B、点C坐标分别为(5,0)、(10,0)、(0,-5).
在平面直角坐标系xOy中,点A、点B、点C坐标分别为(5,0)、(10,0)、(0,-5).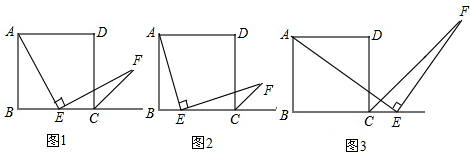
 如图,AB=6,将以AB为直径的半圆再绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为$\frac{9}{2}$π.
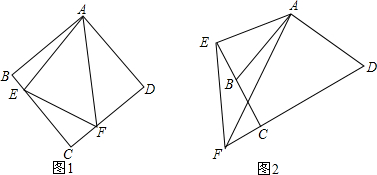
如图,AB=6,将以AB为直径的半圆再绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为$\frac{9}{2}$π.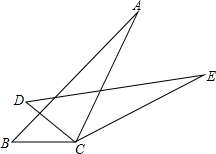 如图所示,∠B=∠D,BC=DC,要判定△ABC≌△EDC,当添加条件∠ACB=∠ECD时,可根据”ASA“判定;当添加条件∠A=∠E时.可根据“AAS”判定;当添加条件AB=ED时,可根据“SAS”判定.
如图所示,∠B=∠D,BC=DC,要判定△ABC≌△EDC,当添加条件∠ACB=∠ECD时,可根据”ASA“判定;当添加条件∠A=∠E时.可根据“AAS”判定;当添加条件AB=ED时,可根据“SAS”判定.