题目内容
13.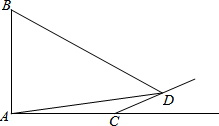 如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:$\sqrt{3}$,求旗杆AB的高度($\sqrt{3}≈1.7$,结果精确到个位).
如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:$\sqrt{3}$,求旗杆AB的高度($\sqrt{3}≈1.7$,结果精确到个位).
分析 延长BD,AC交于点E,过点D作DF⊥AE于点F.构建直角△DEF和直角△CDF.通过解这两个直角三角形求得相关线段的长度即可.
解答  解:延长BD,AC交于点E,过点D作DF⊥AE于点F.
解:延长BD,AC交于点E,过点D作DF⊥AE于点F.
∵i=tan∠DCF=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠DCF=30°.
又∵∠DAC=15°,
∴∠ADC=15°.
∴CD=AC=10.
在Rt△DCF中,DF=CD•sin30°=10×$\frac{1}{2}$=5(米),
CF=CD•cos30°=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$,∠CDF=60°.
∴∠BDF=45°+15°+60°=120°,
∴∠E=120°-90°=30°,
在Rt△DFE中,EF=$\frac{DF}{tanE}$=$\frac{5}{\frac{\sqrt{3}}{3}}$=5$\sqrt{3}$
∴AE=10+5$\sqrt{3}$+5$\sqrt{3}$=10$\sqrt{3}$+10.
在Rt△BAE中,BA=AE•tanE=(10$\sqrt{3}$+10)×$\frac{\sqrt{3}}{3}$=10+$\frac{10\sqrt{3}}{3}$≈16(米).
答:旗杆AB的高度约为16米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.用换元法解方程:$\frac{{x}^{2}-2}{x}$+$\frac{2x}{{x}^{2}-2}$=3时,若设$\frac{{x}^{2}-2}{x}=y$,并将原方程化为关于y的整式方程,那么这个整式方程是( )
| A. | y2-3y+2=0 | B. | y2-3y-2=0 | C. | y2+3y+2=0 | D. | y2+3y-2=0 |
 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm,点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同速度运动,点N到达点C时停止运动,设运动时间为t(s).
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm,点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同速度运动,点N到达点C时停止运动,设运动时间为t(s).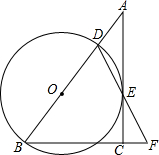 在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O.与AC相切于点E,连结DE并延长与BC的延长线交于点F.
在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O.与AC相切于点E,连结DE并延长与BC的延长线交于点F.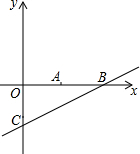 在平面直角坐标系xOy中,点A、点B、点C坐标分别为(5,0)、(10,0)、(0,-5).
在平面直角坐标系xOy中,点A、点B、点C坐标分别为(5,0)、(10,0)、(0,-5).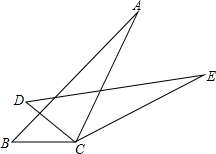 如图所示,∠B=∠D,BC=DC,要判定△ABC≌△EDC,当添加条件∠ACB=∠ECD时,可根据”ASA“判定;当添加条件∠A=∠E时.可根据“AAS”判定;当添加条件AB=ED时,可根据“SAS”判定.
如图所示,∠B=∠D,BC=DC,要判定△ABC≌△EDC,当添加条件∠ACB=∠ECD时,可根据”ASA“判定;当添加条件∠A=∠E时.可根据“AAS”判定;当添加条件AB=ED时,可根据“SAS”判定.