题目内容
2.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
分析 求出所有试验得出来的频率的平均值即可.
解答 解:(1)摸到白球的频率=(0.65+0.62+0.593+0.604+0.601+0.599+0.601)÷7≈0.6,
∴当n很大时,摸到白球的频率将会接近0.6.
故答案为:0.6.
点评 此题主要考查了利用频率估计概率,根据大量反复试验下频率稳定值即概率.用到的知识点为:部分的具体数目=总体数目×相应频率.

练习册系列答案
相关题目
11.《中华人民共和国个人所得税法》规定,公民月工资所得不超过1600元
(人民币)的部分不必纳税,超过1600元的部分为各月应纳税所得额,超过部分的税款按下表分段累加计算.例如,你月工资是2000元,2000-1600=400,那么就对400元进行纳税,400×5%=20,即你应交纳的税款为20元.若某人1月份应交纳此项税款92元,则她当月的工资是多少?
(人民币)的部分不必纳税,超过1600元的部分为各月应纳税所得额,超过部分的税款按下表分段累加计算.例如,你月工资是2000元,2000-1600=400,那么就对400元进行纳税,400×5%=20,即你应交纳的税款为20元.若某人1月份应交纳此项税款92元,则她当月的工资是多少?
| 全月应纳税所得额 | 税率 |
| 不超过500元的部分 | 5% |
| 超过500元至2000元的部分 | 10% |
| 超过2000元至5000元的部分 | 15% |
| 超过5000元至20000元的部分 | 20% |
| … | … |
 如图,在一张长为5cm,宽为4cm的长方形纸片上,现要剪下一个腰长为3cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上),则剪下的等腰三角形的底边的长为3$\sqrt{2}$,2$\sqrt{6}$,$\sqrt{30}$cm.
如图,在一张长为5cm,宽为4cm的长方形纸片上,现要剪下一个腰长为3cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上),则剪下的等腰三角形的底边的长为3$\sqrt{2}$,2$\sqrt{6}$,$\sqrt{30}$cm.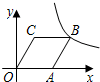 如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )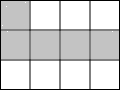 一只蜜蜂将随意落在如图的方格中,每个小方格形状完全相同,则蜜蜂落在阴影部分的概率是$\frac{5}{12}$.
一只蜜蜂将随意落在如图的方格中,每个小方格形状完全相同,则蜜蜂落在阴影部分的概率是$\frac{5}{12}$.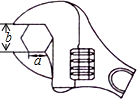 如图,要拧开一个边长为a=6cm的正六边形螺帽,扳手张开的开口b至少为6$\sqrt{3}$acm.
如图,要拧开一个边长为a=6cm的正六边形螺帽,扳手张开的开口b至少为6$\sqrt{3}$acm.