题目内容
10.请观察下列式子,按要求完成下列题目.$\frac{1}{{\sqrt{2}+1}}=\frac{{\sqrt{2}-1}}{{(\sqrt{2}+1)(\sqrt{2}-1)}}=\sqrt{2}-1$;$\frac{1}{{\sqrt{3}+\sqrt{2}}}=\frac{{\sqrt{3}-\sqrt{2}}}{{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}}=\sqrt{3}-\sqrt{2}$;$\frac{1}{{2+\sqrt{3}}}=\frac{{2-\sqrt{3}}}{{(2+\sqrt{3})(2-\sqrt{3})}}=2-\sqrt{3}$;$\frac{1}{{\sqrt{5}+2}}=\frac{{\sqrt{5}-2}}{{(\sqrt{5}+2)(\sqrt{5}-2)}}=\sqrt{5}-2$.
试求:
(1)$\frac{1}{{\sqrt{7}+\sqrt{6}}}$的值;
(2)$\frac{1}{{\sqrt{n+1}+\sqrt{n}}}$(n为正整数)的值;
(3)根据上面的规律,试化简下列式子.$\frac{1}{{\sqrt{2}+1}}$+$\frac{1}{{\sqrt{3}+\sqrt{2}}}$+$\frac{1}{{2+\sqrt{3}}}$+…+$\frac{1}{{\sqrt{2011}+\sqrt{2010}}}$.
分析 (1)分子、分母上下同乘$\sqrt{7}-\sqrt{6}$,即可解答;
(2)分子、分母上下同乘$\sqrt{n+1}-\sqrt{n}$,即可解答;
(3)利用(2)的规律,即可解答.
解答 解:(1)$\frac{1}{\sqrt{7}+\sqrt{6}}=\frac{\sqrt{7}-\sqrt{6}}{(\sqrt{7}+\sqrt{6})(\sqrt{7}-\sqrt{6})}=\sqrt{7}-\sqrt{6}$.
(2)$\frac{1}{{\sqrt{n+1}+\sqrt{n}}}$=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}-\sqrt{n}$.
(3)$\frac{1}{{\sqrt{2}+1}}$+$\frac{1}{{\sqrt{3}+\sqrt{2}}}$+$\frac{1}{{2+\sqrt{3}}}$+…+$\frac{1}{\sqrt{2011}+\sqrt{2010}}$
=$\sqrt{2}-1+\sqrt{3}-\sqrt{2}+2-\sqrt{3}+…+\sqrt{2011}$-$\sqrt{2010}$
=-1$+\sqrt{2011}$.
点评 本题考查分母有理化,解决本题的关键是根据分母有理化,发现规律.

练习册系列答案
相关题目
5.解决下列问题,比较容易用全面调查方式的是( )
| A. | 了解一天大批产品的次品率情况 | B. | 了解某市初中生体育中考的成绩 | ||
| C. | 了解某城市居民的人均收入情况 | D. | 了解某一天离开某市的人口数量 |
15.如表,在3×3的方阵图中,填写了一些数和代数式(其中每个代数式都表示一个数),使得每行的3个数、每列的3个数、斜对角的3个数之和均相等.则每一行的和是( )
| 3 | 4 | x |
| -2 | y | a |
| 2y-x | c | b |
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
2.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
请估计:当n很大时,摸到白球的频率将会接近0.6.(精确到0.1)
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
19.4的平方根是( )
| A. | 2 | B. | 4 | C. | ±2 | D. | ±4 |
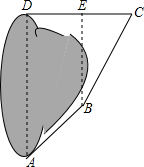 某实践小组去公园测量人工湖AD的长度.小明进行如下测量:点D在点A的正北方向,点B在点A的北偏东50°方向,AB=40米.点E在点B的正北方向,点C在点B的北偏东30°方向,CE=30米.点C和点E都在点D的正东方向,求AD的长(结果精确到1米).(参考数据:$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
某实践小组去公园测量人工湖AD的长度.小明进行如下测量:点D在点A的正北方向,点B在点A的北偏东50°方向,AB=40米.点E在点B的正北方向,点C在点B的北偏东30°方向,CE=30米.点C和点E都在点D的正东方向,求AD的长(结果精确到1米).(参考数据:$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192) 如图,直线a∥b,∠1=45°,则∠2=45°,∠3=135°.
如图,直线a∥b,∠1=45°,则∠2=45°,∠3=135°.