题目内容
17.设x2+mx+121是一个完全平方式,则常数m=±22.分析 先根据两平方项确定出这两个数,再根据完全平方公式的乘积二倍项即可确定m的值.
解答 解:∵x2+mx+121=x2+mx+112,
∴mx=±2•x•11,
解得m=±22.
故答案为:±22.
点评 本题主要考查了完全平方式,根据平方项确定出这两个数是解题的关键,也是难点,熟记完全平方公式对解题非常重要.

练习册系列答案
相关题目
8.为了解某市数学中考成绩,从中随机抽取了3000名考生进行调查,这项调查中的样本是( )
| A. | 某市数学中考成绩 | |
| B. | 从中抽取的3000名考生 | |
| C. | 从中抽取的3000名考生的数学中考成绩 | |
| D. | 3000 |
5.解决下列问题,比较容易用全面调查方式的是( )
| A. | 了解一天大批产品的次品率情况 | B. | 了解某市初中生体育中考的成绩 | ||
| C. | 了解某城市居民的人均收入情况 | D. | 了解某一天离开某市的人口数量 |
12.(-a2)3=( )
| A. | a5 | B. | a6 | C. | -a5 | D. | -a6 |
2.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
请估计:当n很大时,摸到白球的频率将会接近0.6.(精确到0.1)
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
6.方程-4x=1的解是( )
| A. | $x=-\frac{1}{4}$ | B. | x=-4 | C. | $x=\frac{1}{4}$ | D. | x=-4. |
7.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}3x+2y=6\\ \frac{6}{x}-2y=5\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+3y=6\\ y-z=5\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}2x+5y=7\\ xy=5\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+2y=5\\ 3x-2y-5=0\end{array}\right.$ |
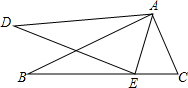 如图,在△ABC和△ADE中,点E在BC上,∠B=∠D,AB=AD,∠EAC=∠DAB
如图,在△ABC和△ADE中,点E在BC上,∠B=∠D,AB=AD,∠EAC=∠DAB 对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.