题目内容
12.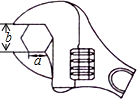 如图,要拧开一个边长为a=6cm的正六边形螺帽,扳手张开的开口b至少为6$\sqrt{3}$acm.
如图,要拧开一个边长为a=6cm的正六边形螺帽,扳手张开的开口b至少为6$\sqrt{3}$acm.
分析 根据题意,即是求该正六边形的边心距的2倍.构造一个由半径、半边、边心距组成的直角三角形,且其半边所对的角是30°,再根据锐角三角函数的知识求解.
解答 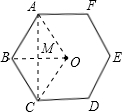 解:设正多边形的中心是O,其一边是AB,
解:设正多边形的中心是O,其一边是AB,
∴∠AOB=∠BOC=60°,
∴OA=OB=AB=OC=BC,
∴四边形ABCO是菱形,
∵AB=6cm,∠AOB=60°,
∴cos∠BAC=$\frac{AM}{AB}$,
∴AM=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$(cm),
∵OA=OC,且∠AOB=∠BOC,
∴AM=MC=$\frac{1}{2}$AC,
∴AC=2AM=6$\sqrt{3}$(cm).
故答案为6$\sqrt{3}$cm.
点评 本题考查了正多边形和圆,构造一个由半径、半边、边心距组成的直角三角形,运用锐角三角函数进行求解是解此题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
2.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
请估计:当n很大时,摸到白球的频率将会接近0.6.(精确到0.1)
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
3.如果关于x的不等式(m+1)x>m+1的解集为x<1,则m的取值范围是( )
| A. | m<0 | B. | m<-1 | C. | m>1 | D. | m>-1 |
7.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}3x+2y=6\\ \frac{6}{x}-2y=5\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+3y=6\\ y-z=5\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}2x+5y=7\\ xy=5\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+2y=5\\ 3x-2y-5=0\end{array}\right.$ |
 如图,每个正方形的边长都是1,点A,C的位置分别用有序数对(3,1),(8,1)表示.
如图,每个正方形的边长都是1,点A,C的位置分别用有序数对(3,1),(8,1)表示. 如图,一个长方形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE的度数是125°,则∠DBC=55°.
如图,一个长方形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE的度数是125°,则∠DBC=55°. 如图是用吸管吸易拉罐内的饮料时的横截面,若∠1=110°,则∠2=70°.(易拉罐的上下底面互相平行)
如图是用吸管吸易拉罐内的饮料时的横截面,若∠1=110°,则∠2=70°.(易拉罐的上下底面互相平行)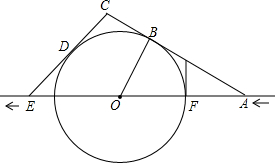 如图,某船在大海中沿航线由东向西行驶,行驶到A时,发现前方20海里的F处出现暗礁,经进一步观察发现前方以点O为圆心(点O在航线上),OF长为半径的区域内充满暗礁,该船马上改变航向,从点A沿北偏西60°方向前进,与⊙O切于点B后到达点C,接着,该船从点C沿南偏西45°方向前进,与⊙O切于点D后回到航线上点E,然后继续沿原航线行驶,请解决下列问题:暗礁区域的半径为多少海里?
如图,某船在大海中沿航线由东向西行驶,行驶到A时,发现前方20海里的F处出现暗礁,经进一步观察发现前方以点O为圆心(点O在航线上),OF长为半径的区域内充满暗礁,该船马上改变航向,从点A沿北偏西60°方向前进,与⊙O切于点B后到达点C,接着,该船从点C沿南偏西45°方向前进,与⊙O切于点D后回到航线上点E,然后继续沿原航线行驶,请解决下列问题:暗礁区域的半径为多少海里?