题目内容
11.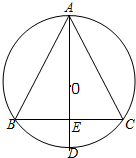 如图,⊙O为△ABC的外接圆,AB=AC,直径AD交BC于点E,DE:AD=1:4,则BE:AB=1:2.
如图,⊙O为△ABC的外接圆,AB=AC,直径AD交BC于点E,DE:AD=1:4,则BE:AB=1:2.
分析 连接BD,由等腰三角形的性质和圆周角定理得出AD⊥BC,∠ABD=90°,证出△ABE∽△BDE,得出对应边成比例BE:AB=DE:BD,设DE=x,则AD=4x,由射影定理求出BD,即可得出结果.
解答 解:连接BD,如图所示: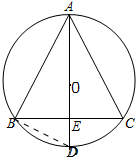
∵AB=AC,直径AD交BC于点E,
∴AD⊥BC,
∵AD是直径,
∴∠ABD=90°,
∴△ABE∽△BDE,
∴BE:AB=DE:BD,
∵DE:AD=1:4,
设DE=x,则AD=4x,
由射影定理得:BD2=DE•AD=4x2,
∴BD=2x,
∴BE:AB=DE:BD=x:2x=1:2;
故答案为:1:2.
点评 本题考查了三角形的外接圆、圆周角定理、等腰三角形的性质、相似三角形的判定与性质、射影定理;证明三角形相似和运用射影定理是解决问题的关键.

练习册系列答案
相关题目
1.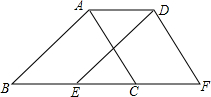 如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )
如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )
 如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )
如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
 平行四边形ABCD的周长为24,对角线AC、BD相交于点O,作OE⊥AC,交AD与点E,连接CE,那么△DEC的周长为12.
平行四边形ABCD的周长为24,对角线AC、BD相交于点O,作OE⊥AC,交AD与点E,连接CE,那么△DEC的周长为12. 如图,BA⊥AC,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为65°.
如图,BA⊥AC,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为65°.