题目内容
2. 平行四边形ABCD的周长为24,对角线AC、BD相交于点O,作OE⊥AC,交AD与点E,连接CE,那么△DEC的周长为12.
平行四边形ABCD的周长为24,对角线AC、BD相交于点O,作OE⊥AC,交AD与点E,连接CE,那么△DEC的周长为12.
分析 由平行四边形ABCD的对角线相交于点O,OE⊥AC,根据线段垂直平分线的性质,可得AE=CE,又由平行四边形ABCD的周长为12,可得AD+CD的长,继而可得△DEC的周长等于AD+CD.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC,AB=CD,AD=BC,
∵平行四边形ABCD的周长为24,
∴AD+CD=12,
∵OE⊥AC,
∴AE=CE,
∴△DEC的周长=CD+CE+DE=CD+CE+AE=CD+AD=12.
故答案为:12.
点评 此题考查了平行四边形的性质以及线段垂直平分线的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
13.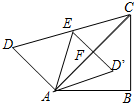 如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )
如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )
 如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )
如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )| A. | $3+\sqrt{3}$ | B. | $3\sqrt{2}+\sqrt{6}$ | C. | $3\sqrt{2}-\sqrt{6}$ | D. | $3-\sqrt{3}$ |
10.已知一次函数y=-2x+3,则与该一次函数的图象关于x轴对称的一次函数的表达式为( )
| A. | y=2x-3 | B. | y=-2x-3 | C. | y=2x+3 | D. | y=-2x+3 |
17.若分式$\frac{{x}^{2}-1}{2x+2}$的值为0,则( )
| A. | x=-1 | B. | x=1 | C. | x=-$\frac{1}{2}$ | D. | x=±1 |
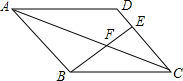 如图,在平行四边形ABCD中,E在DC上,若BF:BE=4:7,则DE:EC=1:3.
如图,在平行四边形ABCD中,E在DC上,若BF:BE=4:7,则DE:EC=1:3.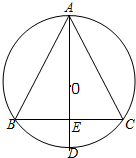 如图,⊙O为△ABC的外接圆,AB=AC,直径AD交BC于点E,DE:AD=1:4,则BE:AB=1:2.
如图,⊙O为△ABC的外接圆,AB=AC,直径AD交BC于点E,DE:AD=1:4,则BE:AB=1:2.