题目内容
3.我们知道:$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$…,那么$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.利用上面的规律计算:$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2009×2011}$=$\frac{1005}{2011}$.
分析 观察给定的等式变形找出规律“两个连续自然数的乘积的倒数=较小数的倒数-较大数的倒数”由此可将$\frac{1}{n(n+1)}$变形为两个分式相减的形式,再由类似的方法找出$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+1}$)这一规律,结合此规律将$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2009×2011}$进行变形即可得出结论.
解答 解:观察$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$…,可发现两个连续自然数的乘积的倒数=较小数的倒数-较大数的倒数,
即$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$.
根据类推法可得出:$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+1}$),
∴$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2009×2011}$=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2009}$-$\frac{1}{2011}$)=$\frac{1}{2}$(1-$\frac{1}{2011}$)=$\frac{1005}{2011}$.
故答案为:$\frac{1}{n}-\frac{1}{n+1}$;$\frac{1005}{2011}$.
点评 本题考查了数字的变化类,解题的关键是找出规律式$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+1}$).本题属于基础题,难度不大,再解决该题型题目时,根据给定等式发现规律是关键.

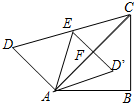 如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )
如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )| A. | $3+\sqrt{3}$ | B. | $3\sqrt{2}+\sqrt{6}$ | C. | $3\sqrt{2}-\sqrt{6}$ | D. | $3-\sqrt{3}$ |
| A. |  | B. |  | C. |  | D. |  |
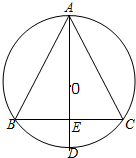 如图,⊙O为△ABC的外接圆,AB=AC,直径AD交BC于点E,DE:AD=1:4,则BE:AB=1:2.
如图,⊙O为△ABC的外接圆,AB=AC,直径AD交BC于点E,DE:AD=1:4,则BE:AB=1:2. 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.则sin∠BAG=$\frac{\sqrt{10}}{10}$.
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.则sin∠BAG=$\frac{\sqrt{10}}{10}$.