题目内容
18．已知x-$\frac{1}{x}$=7，则x2+$\frac{1}{{x}^{2}}$=51．分析 直接利用完全平方公式将已知条件变形求出即可．
解答 解：∵x-$\frac{1}{x}$=7，
∴（x-$\frac{1}{x}$）2=49，
∴x2+$\frac{1}{{x}^{2}}$=51．
故答案为：51．
点评 此题主要考查了完全平方公式，正确应用完全平方公式是解题关键．
练习册系列答案
相关题目
9．计算：a2•（-a）3的结果正确的是（ ）
| A． | -a5 | B． | a5 | C． | -a6 | D． | a6 |
13．若点P（m，n）在第二象限，则点Q（m，-n）在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
3．下列说法错误的是（ ）
| A． | 一组数据的平均数、众数、中位数可能是同一个数 | |
| B． | 一组数据中中位数可能不唯一确定 | |
| C． | 一组数据中平均数、众数、中位数是从不同角度描述了一组数据的集中趋势 | |
| D． | 一组数据中众数可能有多个 |
10．下列运算正确的是（ ）
| A． | $（3-2\sqrt{3}）（3+2\sqrt{3}）={3^2}$-2×3=3 | B． | $（2\sqrt{a}+\sqrt{b}）（\sqrt{a}-\sqrt{b}）=2a-b$ | ||
| C． | ${（3-2\sqrt{3}）^2}={3^2}-{（2\sqrt{3}）^2}$=9-12=-3 | D． | $（\sqrt{a}+\sqrt{a-1}）（\sqrt{a}-\sqrt{a-1}）={（\sqrt{a}）^2}-{（\sqrt{a-1}）^2}$=a-（a-1）=1 |
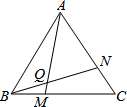如图，已知△ABC中，AB=BC=AC，∠ABC=∠BCA=∠CAB=60°，M、N分别在△ABC的BC、AC边上，且BM=CN，AM、BN交于点Q．求证：∠BQM=60°．