题目内容
10．
已知：如图，在平行四边形ABCD中，AB=AD，对角线AC与BD相交于点O．求证：（1）AB=BC=CD=AD；
（2）AC⊥BD．
分析 （1）直接利用平行四边形的性质得出AD=BC，AB=DC，进而得出答案；
（2）利用线段垂直平分线的判定与性质得出答案．
解答 证明：（1）∵四边形ABCD是平行四边形，
∴AD=BC，AB=DC，
∵AB=AD，
∴AB=BC=CD=AD；
（2）∵AB=BC，CD=AD，
∴BD垂直平分AC，
∴AC⊥BD．
点评 此题主要考查了平行四边形的性质以及线段垂直平分线的判定，正确应用平行四边形的性质是解题关键．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
15．
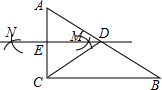如图，在△ABC中，∠ACB=90°，分别以点A和点C为圆心，以相同的长（大于$\frac{1}{2}$AC）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交AC于点E，连接CD．下列结论错误的是（ ）
如图，在△ABC中，∠ACB=90°，分别以点A和点C为圆心，以相同的长（大于$\frac{1}{2}$AC）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交AC于点E，连接CD．下列结论错误的是（ ）| A． | AD=CD | B． | ∠A=∠DCE | C． | ∠ADE=∠DCB | D． | ∠A=2∠DCB |
19．a4-b4和a2+b2的公因式是（ ）
| A． | a2-b2 | B． | a-b | C． | a+b | D． | a2+b2 |
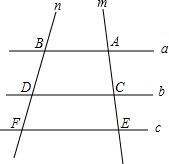如图，已知a∥b∥c，n，m分别与a，b，c交于点B，D，F和点A，C，E，试解决下列问题：