题目内容
10.若整数a使关于x的不等式组$\left\{\begin{array}{l}\frac{x+1}{2}≤\frac{2x+5}{6}\\ x-2>a\end{array}$至少有4个整数解,且使关于x的分式方程$\frac{12-ax}{x+2}$=2有整数解,那么所有满足条件的a的和是( )| A. | -20 | B. | -17 | C. | -14 | D. | -23 |
分析 根据不等式组求出a的范围,然后再根据分式方程求出a的范围,从而确定的a的可能值.
解答 解:不等式组整理得:$\left\{\begin{array}{l}{x≤2}\\{x>a+2}\end{array}\right.$,
由不等式组至少有4个整数解,得到a+2<-1,
解得:a<-3,
分式方程去分母得:12-ax=2x+4,
解得:x=$\frac{8}{a+2}$,
∵分式方程有整数解,
∴a+2=±1、±2、±4、±8,
即a=-1、-3、0、-4、2、-6、6、-10,
又∵x=$\frac{8}{a+2}$≠-2,
∴a≠-6,
由a<-3得:a=-10或-4,
∴所有满足条件的a的和是-14,
故选C.
点评 本题考查学生的计算能力以及推理能,解题的关键是根据不等式组以及分式方程求出a的范围,本题属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.若要使4a2+mab+9b2是完全平方式,则m的值应为( )
| A. | ±12 | B. | -3 | C. | 12 | D. | -$\frac{1}{3}$ |
2.已知m,n是方程x2-2x-1=0的两实数根,则$\frac{1}{m}$+$\frac{1}{n}$的值为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
19.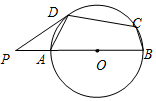 如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )
 如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
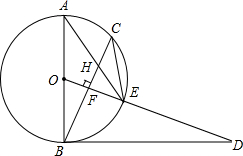 如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC. 如图,AB∥CD,AF∥ED,判断∠A与∠D是否相等,并说明理由.
如图,AB∥CD,AF∥ED,判断∠A与∠D是否相等,并说明理由.