题目内容
18．计算：$\sqrt{4}$+$\root{3}{64}$-|-$\sqrt{2}$|分析 首先计算开方，然后从左向右依次计算，求出算式的值是多少即可．
解答 解：$\sqrt{4}$+$\root{3}{64}$-|-$\sqrt{2}$|
=2+4-$\sqrt{2}$
=6-$\sqrt{2}$
点评 此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．
练习册系列答案
活力课时同步练习册系列答案
相关题目
6．下列几个式子：其中y是x的函数的是（ ）
| A． | y=2x | B． | y2=2x | C． | y=±2x | D． | |y|=2x |
13．在二次函数y=x2+bx+c中，函数y与自变量x之间的部分对应值如下表所示：
若点A（-1，m），B（6，n），则m＞n．（选填“＞”、“＜”或“=”）
| x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
3．计算（-a）3•（a2）3的结果正确的是（ ）
| A． | a11 | B． | -a11 | C． | -a9 | D． | a8 |
10．若整数a使关于x的不等式组$\left\{\begin{array}{l}\frac{x+1}{2}≤\frac{2x+5}{6}\\ x-2＞a\end{array}$至少有4个整数解，且使关于x的分式方程$\frac{12-ax}{x+2}$=2有整数解，那么所有满足条件的a的和是（ ）
| A． | -20 | B． | -17 | C． | -14 | D． | -23 |
7．下列各式中计算正确的是（ ）
| A． | （x+y）2=x2+y2 | B． | 3x2=6x2 | C． | a2+a2=a4 | D． | （x2）3=x6 |
8．
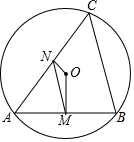如图，△ABC内接于⊙O，OM⊥AB，ON⊥AC，垂足分别为M，N，连接MN，若AB=4，AC=6，∠A=60°．设MN=m，则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是（ ）
如图，△ABC内接于⊙O，OM⊥AB，ON⊥AC，垂足分别为M，N，连接MN，若AB=4，AC=6，∠A=60°．设MN=m，则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是（ ）| A． | 2$\sqrt{3}$ | B． | 2$\sqrt{2}$ | C． | $\frac{1}{2}$$\sqrt{3}$ | D． | $\frac{1}{2}\sqrt{2}$ |