题目内容
12．实数a，b，c，d在数轴上的对应点从左到右依次是A，B，C，D，若b+d=0，则a+c的值（ ）| A． | 小于0 | B． | 等于0 | ||
| C． | 大于0 | D． | 与a，b，c，d的取值有关 |
分析 根据数轴上的点表示的是右边的总比左边的大，可得答案．
解答 解：∵A在B的左边，C在D的左边，
∴a＜b，c＜d，
∴a+c＜b+d=0，
故选：A．
点评 本题考查了实数与数轴，利用数轴上的点表示的是右边的总比左边的大得出a＜b，c＜d是解题关键，又利用了不等式的性质．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
2．给定下列条件，不能判定△ABC是直角三角形的是（ ）
| A． | ∠A=∠B=2∠C | B． | ∠A+∠B=∠C | C． | ∠A：∠B：∠C=1：4：5 | D． | ∠A=37°，∠B=53° |
如图，在正方形ABCD中，AB=4$\sqrt{2}$，AC与BD相交于点O，点P是AC上一动点，点E为射线BC上的一点，且PB=PE，过点E作EF⊥AC，垂足为点F．
20．-$\frac{1}{5}$相反数的倒数是（ ）
| A． | $-\frac{1}{5}$ | B． | $\frac{1}{5}$ | C． | 5 | D． | -5 |
17．
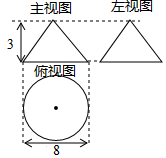已知一个圆锥体的三视图如图所示，则这个圆锥体的侧面积是（ ）
已知一个圆锥体的三视图如图所示，则这个圆锥体的侧面积是（ ）| A． | 40π | B． | 24π | C． | 20 π | D． | 12π |
4．
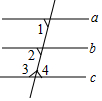如图，下列推理错误的是（ ）
如图，下列推理错误的是（ ）| A． | ∵∠1=∠2，∴a∥b | B． | ∵b∥c，∴∠2=∠4 | ||
| C． | ∵a∥b，b∥c，∴a∥c | D． | ∵∠2+∠3=180°，∴a∥c |
1．4cos60°的值为（ ）
| A． | $\frac{1}{2}$ | B． | 2 | C． | $\frac{\sqrt{3}}{2}$ | D． | 2$\sqrt{3}$ |
如图，已知菱形ABCD的对角线AC，BD相交于点O，延长AB至点E，使BE=AB，连接CE．