题目内容
14.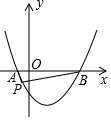 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )| A. | -1<m<0 | B. | -1<m<0或3<m<4 | C. | 0<m<3或m>4 | D. | m<-1或0<m<3 |
分析 根据解析式求得点A、B的坐标,以AB为直径作圆M,与y轴交于点P,因为AB为直径,所以当抛物线上的点P在⊙M的内部时,满足∠APB为钝角,进而得出m的取值范围.
解答 解:令y=0得:$\frac{1}{2}$x2-$\frac{3}{2}$x-2=0,
解得:x=-1或x=4,
则点A(-1,0)、B(4,0),
以AB为直径作圆M,与y轴交于点P.则抛物线在圆内的部分如图所示,能使∠APB为钝角,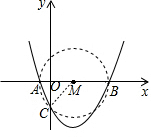
∴M($\frac{3}{2}$,0),⊙M的半径=$\frac{5}{2}$.
在Rt△OMP中,∴OP=$\sqrt{P{M}^{2}-O{M}^{2}}$=2.
∴P(0,-2),
由抛物线的对称性可知,P′(3,-2),
∴当-1<m<0或3<m<4时,∠APB为钝角,
故选:B.
点评 本题考查了抛物线与x轴的交点与圆周角定理,注意数形结合利用圆周角定理得出P点坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.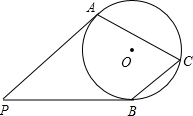 如图,PA,PB是⊙O的切线,切点分别为A,B,点C在⊙O上,且$\widehat{ACB}$是优弧,则∠ACB等于( )
如图,PA,PB是⊙O的切线,切点分别为A,B,点C在⊙O上,且$\widehat{ACB}$是优弧,则∠ACB等于( )
 如图,PA,PB是⊙O的切线,切点分别为A,B,点C在⊙O上,且$\widehat{ACB}$是优弧,则∠ACB等于( )
如图,PA,PB是⊙O的切线,切点分别为A,B,点C在⊙O上,且$\widehat{ACB}$是优弧,则∠ACB等于( )| A. | 180°-2∠P | B. | 180°-∠P | C. | 90°-$\frac{1}{2}$∠P | D. | ∠P |
2.给定下列条件,不能判定△ABC是直角三角形的是( )
| A. | ∠A=∠B=2∠C | B. | ∠A+∠B=∠C | C. | ∠A:∠B:∠C=1:4:5 | D. | ∠A=37°,∠B=53° |
9.如果三角形的两边长分别为3和6,第三边长是奇数,则第三边长可以是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 9 |
19.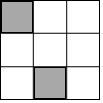 如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,能使三个被涂黑的小正方形组成一个轴对称图形的概率是( )
如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,能使三个被涂黑的小正方形组成一个轴对称图形的概率是( )
 如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,能使三个被涂黑的小正方形组成一个轴对称图形的概率是( )
如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,能使三个被涂黑的小正方形组成一个轴对称图形的概率是( )| A. | $\frac{5}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{2}{7}$ |
6.为了解某市参加中考的45000名学生的身高情况,抽查了其中1500名学生的身高进行统计分析.下面叙述正确的是( )
| A. | 45000名学生是总体 | |
| B. | 1500名学生的身高是总体的一个样本 | |
| C. | 每名学生是总体的一个个体 | |
| D. | 以上调查是全面调查 |
4.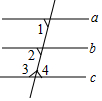 如图,下列推理错误的是( )
如图,下列推理错误的是( )
 如图,下列推理错误的是( )
如图,下列推理错误的是( )| A. | ∵∠1=∠2,∴a∥b | B. | ∵b∥c,∴∠2=∠4 | ||
| C. | ∵a∥b,b∥c,∴a∥c | D. | ∵∠2+∠3=180°,∴a∥c |
 如图,在正方形ABCD中,AB=4$\sqrt{2}$,AC与BD相交于点O,点P是AC上一动点,点E为射线BC上的一点,且PB=PE,过点E作EF⊥AC,垂足为点F.
如图,在正方形ABCD中,AB=4$\sqrt{2}$,AC与BD相交于点O,点P是AC上一动点,点E为射线BC上的一点,且PB=PE,过点E作EF⊥AC,垂足为点F.