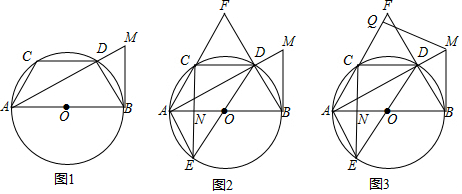
��Ŀ����
8������������y=ax2+4ax+m��x��Ľ���ΪA��-1��0����B��x2��0����������˵������һԪ���η���ax2+4ax+m=0������Ϊx1=-1��x2=-3
��ԭ��������y�ύ��C�㣬CD��x�ύ��������D�㣬��CD=4
�۵�E��1��y1������F��-3��y2����ԭ�������ϣ���y2��y1
��������y=ax2-4ax+m��ԭ�����߹���y��Գƣ�
������ȷ���ǣ�������
| A�� | �٢ڢۢ� | B�� | �٢ڢ� | C�� | �٢� | D�� | �٢ڢ� |
���� �������ߵĶԳ���x=-2������x��Ľ���A��-1��0�������öԳ��Կɵ���һ���㼴���жϢ٣����������ߵĶԳ��Լ��Գ���x=-2�ɵ�CD�ij��������жϢڣ�������������x��Ľ��㼰���κ����������ԣ���Ͽ��ڷ�����жϢۣ����ݹ���y��ĶԳƵ�ͼ�κ����껥Ϊ�෴������������ȿ��жϢܣ�
��� �⣺��������y=ax2+4ax+m�ĶԳ���Ϊx=-$\frac{4a}{2a}$=-2��
������������x��Ľ���A��-1��0��֪��������x�����һ������B������Ϊ��-3��0����
��һԪ���η���ax2+4ax+m=0������Ϊx1=-1��x2=-3���ʢ���ȷ��
�������⣬��C��0��m����D��n��m����
�������ߵĶԳ���Ϊx=-2֪$\frac{0+n}{2}$=-2����n=-4��
��CD=|n-0|=|n|=4���ʢ���ȷ��
������֪����x=-3ʱ��y1=0��
���������߿�������ʱ����x=1����y2��0����y2��y1��
�������߿�������ʱ����x=1����y2��0����y2��y1���ʢ۴���
������y=ax2+4ax+m����y��ԳƵ�������Ϊy=a��-x��2+4a•��-x��+m=ax2-4ax+m���ʢ���ȷ��
���ϣ���ȷ���Ǣ٢ڢܣ�
��ѡ��B��
���� ������Ҫ������������x��Ľ������⣬�������ն��κ�����ͼ���������ǽ���Ĺؼ���

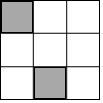 ��ͼ����3��3�������������У���������С�����α�Ϳ�ڣ��ٽ�ͼ������С����������Ϳ��һ������ʹ������Ϳ�ڵ�С���������һ����Գ�ͼ�εĸ����ǣ�������
��ͼ����3��3�������������У���������С�����α�Ϳ�ڣ��ٽ�ͼ������С����������Ϳ��һ������ʹ������Ϳ�ڵ�С���������һ����Գ�ͼ�εĸ����ǣ�������| A�� | $\frac{5}{7}$ | B�� | $\frac{4}{7}$ | C�� | $\frac{3}{7}$ | D�� | $\frac{2}{7}$ |
| A�� | $-\frac{1}{5}$ | B�� | $\frac{1}{5}$ | C�� | 5 | D�� | -5 |
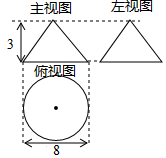 ��֪һ��Բ�������ͼ��ͼ��ʾ�������Բ��IJ�����ǣ�������
��֪һ��Բ�������ͼ��ͼ��ʾ�������Բ��IJ�����ǣ�������| A�� | 40�� | B�� | 24�� | C�� | 20 �� | D�� | 12�� |
| A�� | ���� | B�� | ��λ�� | C�� | ���� | D�� | ���϶����� |
 ��ͼ����������ABCD�У�AB=4$\sqrt{2}$��AC��BD�ཻ�ڵ�O����P��AC��һ���㣬��EΪ����BC�ϵ�һ�㣬��PB=PE������E��EF��AC������Ϊ��F��
��ͼ����������ABCD�У�AB=4$\sqrt{2}$��AC��BD�ཻ�ڵ�O����P��AC��һ���㣬��EΪ����BC�ϵ�һ�㣬��PB=PE������E��EF��AC������Ϊ��F��