题目内容
19.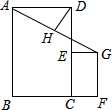 如图,已知四边形ABCD与四边形CFGE都是矩形,点E在CD上,点H为AG的中点,AB=3,BC=2,CE=1.5,CF=1,则DH的长为$\frac{\sqrt{13}}{4}$.
如图,已知四边形ABCD与四边形CFGE都是矩形,点E在CD上,点H为AG的中点,AB=3,BC=2,CE=1.5,CF=1,则DH的长为$\frac{\sqrt{13}}{4}$.
分析 延长GE交AB于点M,作DN⊥AG于N.首先求出AG、AH,由ADN∽△GAM,得$\frac{AD}{AG}$=$\frac{AN}{MG}$=$\frac{DN}{AM}$,求出DN、AN,HN,在Rt△DHN中利用勾股定理即可解决问题.
解答 解:延长GE交AB于点M,作DN⊥AG于N.
∵四边形ABCD与四边形CFGE都是矩形,
∴四边形BFGM是矩形,
∴MG=BF=BC+CF=2+1=3,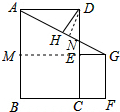
∴BM=CE=FG=1.5,
∴AM=AB-BM=1.5,
∴AG=$\sqrt{A{M}^{2}+G{M}^{2}}$=$\frac{3}{2}$$\sqrt{5}$,
∵点H为AG的中点,
∴AH=$\frac{1}{2}$AG=$\frac{3}{4}$$\sqrt{5}$,
∵AD∥MG,
∴∠DAN=∠AGM,∵∠AND=∠AMG,
∴△ADN∽△GAM,
∴$\frac{AD}{AG}$=$\frac{AN}{MG}$=$\frac{DN}{AM}$,
∴$\frac{2}{\frac{3}{2}\sqrt{5}}$=$\frac{AN}{3}$=$\frac{DN}{\frac{3}{2}}$,
∴AN=$\frac{4}{5}$$\sqrt{5}$,DN=$\frac{2}{5}$$\sqrt{5}$,
∴HN=AN=AH=$\frac{4}{5}$$\sqrt{5}$-$\frac{3}{4}$$\sqrt{5}$=$\frac{1}{20}$$\sqrt{5}$,
∴在Rt△DHN中,DH=$\sqrt{D{N}^{2}+H{N}^{2}}$=$\sqrt{\frac{4}{5}+\frac{1}{80}}$=$\frac{\sqrt{13}}{4}$.
故答案为$\frac{\sqrt{13}}{4}$.
点评 本题考查矩形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

 随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:
随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:| 乘车路程计价区段 | 0-10 | 11-15 | 16-20 | … |
| 对应票价(元) | 2 | 3 | 4 | … |
一位家住十渡地区的张老师持卡乘车,上车时站名上对应的数字是6,下车时站名上对应的数字是24,那么,张老师乘车的费用是2元.
 如图,四边形ABCD内接于圆,则该圆的圆心可以这样确定( )
如图,四边形ABCD内接于圆,则该圆的圆心可以这样确定( )| A. | 线段AC,BD的交点即是圆心 | |
| B. | 线段BD的中点即是圆心 | |
| C. | ∠A与∠B的角平分线交点即是圆心 | |
| D. | 线段AD,AB的垂直平分线的交点即是圆心 |
 如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=36°,则∠ABF=54°.
如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=36°,则∠ABF=54°.

 如图,在⊙O中,圆心角∠AOB=100°,点P是$\widehat{AB}$上任意一点(不与A、B重合,点C在AP的延长线上),则∠BPC=50°.
如图,在⊙O中,圆心角∠AOB=100°,点P是$\widehat{AB}$上任意一点(不与A、B重合,点C在AP的延长线上),则∠BPC=50°.