题目内容
4.如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,设△B3D2C2的面积为S2,…,设△Bn+1DnCn的面积为Sn,则S2=$\frac{\sqrt{3}}{2}$,Sn=$\frac{\sqrt{3}n}{n+1}$(用含n的式子表示).
分析 由三角形的相似性可求得S2、S3、S4的值,则Sn的值也可用含n的式子表示出来.
解答 解:n+1个边长为2的等边三角形有一条边在同一直线上,则B1,B2,B3,…Bn在一条直线上,作出直线B1B2.
∴S△AB1C1=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
∵∠B1C1B2=60°,
∴AB1∥B2C1,
∴△B1C1B2是等边△,且边长=2,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1=$\frac{\sqrt{3}}{2}$,
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2=$\frac{2\sqrt{3}}{3}$,
同理:BnBn+1:ACn=1:n,
∴BnDn:DnCn=1:n,
∴Sn=$\frac{\sqrt{3}n}{n+1}$.
故答案为:$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}n}{n+1}$.
点评 此题考查了相似三角形的判定与性质以及等边三角形的性质,此题难度较大,属于规律性题目,注意辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 如图,线段AB的长为5,C为线段AB上一动点(与点A、B不重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形ACD和BCE,若AD=x,BE=y,那么x2+y2最小值是$\frac{25}{4}$.
如图,线段AB的长为5,C为线段AB上一动点(与点A、B不重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形ACD和BCE,若AD=x,BE=y,那么x2+y2最小值是$\frac{25}{4}$.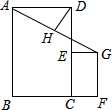 如图,已知四边形ABCD与四边形CFGE都是矩形,点E在CD上,点H为AG的中点,AB=3,BC=2,CE=1.5,CF=1,则DH的长为$\frac{\sqrt{13}}{4}$.
如图,已知四边形ABCD与四边形CFGE都是矩形,点E在CD上,点H为AG的中点,AB=3,BC=2,CE=1.5,CF=1,则DH的长为$\frac{\sqrt{13}}{4}$. 如图,为一块面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,现要把它加工成正方形DEFG木板(EF在AC上,点D和点G分别在AB和BC上),则该正方形木板的边长为$\frac{30}{37}$m.
如图,为一块面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,现要把它加工成正方形DEFG木板(EF在AC上,点D和点G分别在AB和BC上),则该正方形木板的边长为$\frac{30}{37}$m. 如图,在正方形ABCD中,点E,F分别在AB,BC上,且AE=CF,BE=2AE,连接DE,FG⊥DE,垂足为点G,连接CG,则tan∠FGC的值是$\frac{1}{3}$.
如图,在正方形ABCD中,点E,F分别在AB,BC上,且AE=CF,BE=2AE,连接DE,FG⊥DE,垂足为点G,连接CG,则tan∠FGC的值是$\frac{1}{3}$.