题目内容
7.如图所示,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则S2016=$\frac{1008}{2017}$.
分析 连接B1、B2、B3、B4点,显然它们共线且平行于AC1,依题意可知△B1C1B2是等腰直角三角形,知道△B1B2D1与△C1AD1相似,求出相似比,根据三角形面积公式可得出S1,同理:B2B3:AC2=1:2,所以B2D2:D2C2=1:2,所以S2=$\frac{2}{3}$×$\frac{1}{2}$=$\frac{1}{3}$,同样的道理,即可求出S3,sn,得到答案.
解答 解:∵n+1个边长为1的等腰三角形有一条边在同一直线上,
∴S△AB1C1=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
连接B1、B2、B3、B4点,显然它们共线且平行于AC1
∵∠B1C1B2=90°
∴A1B1∥B2C1
∴△B1C1B2是等腰直角三角形,且边长=1,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1=$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$=$\frac{1}{2×(1+1)}$,
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2=$\frac{2}{3}$×$\frac{1}{2}$=$\frac{1}{3}$=$\frac{2}{2×(2+1)}$,
…
sn=$\frac{n}{2(n+1)}$,
则S2016=$\frac{2016}{2×(2016+1)}$=$\frac{1008}{2017}$,
故答案为:$\frac{1008}{2017}$.
点评 本题主要考查相似三角形的判定和性质,等腰直角三角形的定义和性质、三角形的面公式等知识点、本题关键在于作好辅助线,得到相似三角形,求出相似比,就很容易得出答案了,意在提高同学们总结归纳的能力.

练习册系列答案
相关题目
16.已知一个两位数的个位数字是y,十位数字是x,则这个两位数是( )
| A. | x+y | B. | xy | C. | 10+y | D. | 10xy |

 如图,线段AB的长为5,C为线段AB上一动点(与点A、B不重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形ACD和BCE,若AD=x,BE=y,那么x2+y2最小值是$\frac{25}{4}$.
如图,线段AB的长为5,C为线段AB上一动点(与点A、B不重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形ACD和BCE,若AD=x,BE=y,那么x2+y2最小值是$\frac{25}{4}$.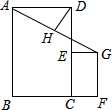 如图,已知四边形ABCD与四边形CFGE都是矩形,点E在CD上,点H为AG的中点,AB=3,BC=2,CE=1.5,CF=1,则DH的长为$\frac{\sqrt{13}}{4}$.
如图,已知四边形ABCD与四边形CFGE都是矩形,点E在CD上,点H为AG的中点,AB=3,BC=2,CE=1.5,CF=1,则DH的长为$\frac{\sqrt{13}}{4}$. 如图,为一块面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,现要把它加工成正方形DEFG木板(EF在AC上,点D和点G分别在AB和BC上),则该正方形木板的边长为$\frac{30}{37}$m.
如图,为一块面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,现要把它加工成正方形DEFG木板(EF在AC上,点D和点G分别在AB和BC上),则该正方形木板的边长为$\frac{30}{37}$m.