题目内容
7.某游乐场在暑假期间推出学生个人门票优惠价,各票价如下:| 票价种类 | (A)夜场通宵 | (B)白天通场 |
| 单价(元) | 50 | 80 |
(1)写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W与x之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不超过30张,且购票总费用不超过7160元,则有几种购票方案?并指出哪种方案费用最少.
分析 (1)由慈善机构欲购买两种类型的票共100张奖励品学兼优的留守学生,可知x+y=100,变形后即可得出结论;
(2)根据购票总费用=购买A种票的张数×A种票的单价+购买B种票的张数×B种票的单价,由此即可得出W关于x的函数关系上;
(3)结合(2)结论以及购买的学生夜场票不超过30张,且购票总费用不超过7160元,可得出关于x的一元一次不等式组,解不等式组即可得出x的取值范围,再利用一次函数的性质即可得出结论.
解答 解:(1)由已知得:x+y=100,
∴y=-x+100.
(2)根据题意可知:
W=50x+80(-x+100)=-30x+8000(0≤x≤100).
(3)由已知得:$\left\{\begin{array}{l}{x≤30}\\{-30x+8000≤7160}\end{array}\right.$,
解得:28≤x≤30.
∴共有3种购票方案:
方案一:购买A种票28张、B种票72张;方案二:购买A种票29张、B种票71张;方案三:购买A种票30张、B种票70张.
∵在W=-30x+8000中,k=-30<0,
∴W随着x的增大而减小,
∴方案三:购买A种票30张、B种票70张所花费用最少.
点评 本题考查了一次函数的应用以及解一元一次不等式组,解题的关键是:(1)根据数量关系找出x、y之间的关系;(2)根据数量关系找出W关于x的函数关系式;(3)根据数量关系找出关于x的一元一次不等式组.本题属于基础题,难度不大,解决该题型题目时,根据数量关系找出函数关系式(不等式或不等式组)是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知数据:6,6,x,4的众数与平均数相等,那么这组数据的极差是( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
15.点P是第二象限的点且到x轴的距离为3、到y轴的距离为4,则点P的坐标是( )
| A. | (-4,3) | B. | ( 4,-3) | C. | ( 3,-4) | D. | (-3,4). |
 如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+
如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+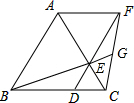 如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论: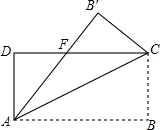 如图,在矩形ABCD中,AB=8,BC=4,将矩形AC折叠,点B落在点B′处,重叠部分△AFC的面积为( )
如图,在矩形ABCD中,AB=8,BC=4,将矩形AC折叠,点B落在点B′处,重叠部分△AFC的面积为( )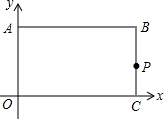 如图,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x-6中上的一点.若△APD是等腰Rt△,则点D的坐标为(4,2)或($\frac{20}{3}$,$\frac{22}{3}$)或($\frac{28}{3}$,$\frac{38}{3}$).
如图,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x-6中上的一点.若△APD是等腰Rt△,则点D的坐标为(4,2)或($\frac{20}{3}$,$\frac{22}{3}$)或($\frac{28}{3}$,$\frac{38}{3}$).