如图.在边长为1的正方形ABCD的边上有一个动点P.点P由点A沿着折线ABCD向点D移动.设点P移动的路程为x.△DAP的面积为S.求S与x的函数关系．题目和参考答案——青夏教育精英家教网—

题目内容

15．

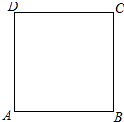如图，在边长为1的正方形ABCD的边上有一个动点P，点P由点A（起点）沿着折线ABCD向点D（终点）移动，设点P移动的路程为x，△DAP的面积为S，求S与x的函数关系．

分析根据题意和图形结合三角形的面积公式，从点P的三个不同位置求出面积即可．

解答解：当0＜x≤1时，S=$\frac{1}{2}$x；
当1＜x≤2时，S=$\frac{1}{2}$
当2＜x＜3时，S=-$\frac{1}{2}$x+$\frac{3}{2}$

点评本题考查的是根据图形求出函数关系式，灵活运用分类讨论思想、数形结合思想是解题的关键．

练习册系列答案

相关题目

5．

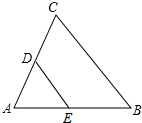如图，在△ABC中，D、E分别是边AC、AB上的点，下列命题中，假命题是（　　）

	A．	若$\frac{AD}{AC}$=$\frac{DE}{BC}$，则△ADE与△ABC相似		B．	若$\frac{AD}{DC}$=$\frac{AE}{EB}$，则△ADE与△ABC相似
	C．	若$\frac{AD}{AB}$=$\frac{AE}{AC}$，则△ADE与△ABC相似		D．	若∠ADE=∠B，则△ADE与△ABC相似

6．①分解因式：（2a-b）²+8ab
②求x的值：4（x-1）²=9．

3．

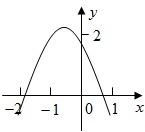如图，二次函数y=ax²+bx+c（a≠0）的图象经过点（-1，2），且与X轴交点的横坐标分别为x₁，x₂，其中-2＜x₁＜-1，0＜x₂＜1，下列结论：
①4a-2b+c＜0；②2a-b＜0；③a+c＜1；④b²+8a＞4ac，
其中正确的有（　　）

10．计算：
（1）3$\sqrt{2}$+|$\sqrt{2}-\sqrt{3}$|-2$\sqrt{2}$．
（2）$\sqrt{169}$+$\root{3}{-8}$-（-$\sqrt{3}$）²．
（3）（-3）²×（-2）²÷4÷2+$\sqrt{（-2）^{6}}$÷（-4）×2．
（4）-$\root{3}{-（-2）^{3}}$÷$\sqrt{2\frac{1}{4}}$÷$\root{3}{（-1）^{100}}$．

20．解方程或方程组：
（1）$\frac{x+3}{0.2}$-$\frac{0.4x-1}{0.5}$=-2.5；
（2）$\left\{\begin{array}{l}{\frac{2x-y}{3}-\frac{x+y}{4}=-\frac{1}{12}}\\{3（x+y）-2（2x-y）=3}\end{array}$．

7．已知矩形ABCD中，AB=2BC，在CD上取一点E，使得∠EAB=30°，AE=AB，则∠EBC的度数为（　　）

x³+x²=x⁵

（x²）³=x⁶

x³•x²=x⁶

5．已知二次函数y=（x-1）²-t²（t≠0），方程（x-1）²-t²-1=0的两根分别为m，n（m＜n），方程（x-1）²-t²-2=0的两根分别为p，q（p＜q），判断m，n，p，q的大小关系是p＜m＜n＜q（用“＜”连接）

试题分类