题目内容
20.解方程或方程组:(1)$\frac{x+3}{0.2}$-$\frac{0.4x-1}{0.5}$=-2.5;
(2)$\left\{\begin{array}{l}{\frac{2x-y}{3}-\frac{x+y}{4}=-\frac{1}{12}}\\{3(x+y)-2(2x-y)=3}\end{array}$.
分析 (1)方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解;
(2)方程组整理后利用加减消元法求出解即可.
解答 解:(1)方程组整理得:$\frac{10x+30}{2}$-$\frac{4x-10}{5}$=-2.5,
去分母得:50x+150-8x+20=-25,
移项合并得:42x=-195,
解得:x=-$\frac{65}{14}$;
(2)方程组整理得:$\left\{\begin{array}{l}{5x-7y=-1①}\\{-x+y=3②}\end{array}\right.$,
①+②×5得:-2y=14,即y=-7,
把y=-7代入②得:x=-10,
则方程组的解为$\left\{\begin{array}{l}{x=-10}\\{y=-7}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
8. 如图,在正△ABC中,D、E分别在AC、AB上,且$\frac{AD}{AC}=\frac{1}{3}$,AE=BE,则有( )
如图,在正△ABC中,D、E分别在AC、AB上,且$\frac{AD}{AC}=\frac{1}{3}$,AE=BE,则有( )
 如图,在正△ABC中,D、E分别在AC、AB上,且$\frac{AD}{AC}=\frac{1}{3}$,AE=BE,则有( )
如图,在正△ABC中,D、E分别在AC、AB上,且$\frac{AD}{AC}=\frac{1}{3}$,AE=BE,则有( )| A. | △AED∽△ABC | B. | △ADB∽△BED | C. | △BCD∽△ABC | D. | △AED∽△CBD |
10.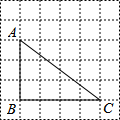 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA=( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA=( )
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA=( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA=( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
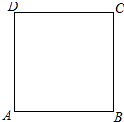 如图,在边长为1的正方形ABCD的边上有一个动点P,点P由点A(起点)沿着折线ABCD向点D(终点)移动,设点P移动的路程为x,△DAP的面积为S,求S与x的函数关系.
如图,在边长为1的正方形ABCD的边上有一个动点P,点P由点A(起点)沿着折线ABCD向点D(终点)移动,设点P移动的路程为x,△DAP的面积为S,求S与x的函数关系.