题目内容
10.计算:(1)3$\sqrt{2}$+|$\sqrt{2}-\sqrt{3}$|-2$\sqrt{2}$.
(2)$\sqrt{169}$+$\root{3}{-8}$-(-$\sqrt{3}$)2.
(3)(-3)2×(-2)2÷4÷2+$\sqrt{(-2)^{6}}$÷(-4)×2.
(4)-$\root{3}{-(-2)^{3}}$÷$\sqrt{2\frac{1}{4}}$÷$\root{3}{(-1)^{100}}$.
分析 (1)原式利用绝对值的代数意义化简,合并即可;
(2)原式利用平方根,立方根定义计算即可得到结果;
(3)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(4)原式利用平方根及立方根定义计算即可得到结果.
解答 解:(1)原式=3$\sqrt{2}$+$\sqrt{3}$-$\sqrt{2}$-2$\sqrt{2}$=$\sqrt{3}$;
(2)原式=13-2-3=8;
(3)原式=9×4×$\frac{1}{4}$×$\frac{1}{2}$+8×(-$\frac{1}{4}$)×2=$\frac{9}{2}$-4=$\frac{1}{2}$;
(4)原式=-2×$\frac{2}{3}$×1=-$\frac{4}{3}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
20.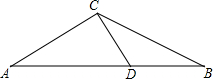 △ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,则∠A的度数是( )
△ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,则∠A的度数是( )
 △ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,则∠A的度数是( )
△ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,则∠A的度数是( )| A. | 22.5° | B. | 30° | C. | 36° | D. | 45° |
19.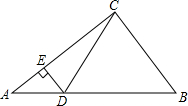 如图,在Rt△ABC中,∠ACB=90°,tanB=$\frac{4}{3}$,点D,E分别在边AB,AC上,DE⊥AC,DE=6,DB=20,则tan∠BCD的值是$\frac{8}{3}$.
如图,在Rt△ABC中,∠ACB=90°,tanB=$\frac{4}{3}$,点D,E分别在边AB,AC上,DE⊥AC,DE=6,DB=20,则tan∠BCD的值是$\frac{8}{3}$.
 如图,在Rt△ABC中,∠ACB=90°,tanB=$\frac{4}{3}$,点D,E分别在边AB,AC上,DE⊥AC,DE=6,DB=20,则tan∠BCD的值是$\frac{8}{3}$.
如图,在Rt△ABC中,∠ACB=90°,tanB=$\frac{4}{3}$,点D,E分别在边AB,AC上,DE⊥AC,DE=6,DB=20,则tan∠BCD的值是$\frac{8}{3}$.
20.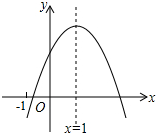 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )| A. | abc<0 | B. | 2a+b=0 | C. | b2-4ac>0 | D. | a-b+c>0 |
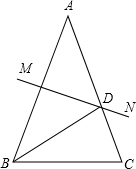 如图所示,AB=AC,∠A=50°,AB,的垂直平分线MN交AC于D,则∠DBC的度数是15°.
如图所示,AB=AC,∠A=50°,AB,的垂直平分线MN交AC于D,则∠DBC的度数是15°.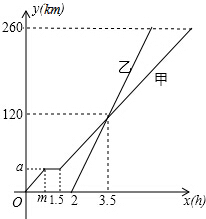 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法: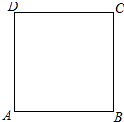 如图,在边长为1的正方形ABCD的边上有一个动点P,点P由点A(起点)沿着折线ABCD向点D(终点)移动,设点P移动的路程为x,△DAP的面积为S,求S与x的函数关系.
如图,在边长为1的正方形ABCD的边上有一个动点P,点P由点A(起点)沿着折线ABCD向点D(终点)移动,设点P移动的路程为x,△DAP的面积为S,求S与x的函数关系. 如图,求∠A+∠B+∠C+∠D+∠E+∠F 的度数(提示:构造四边形,利用多边形内角和求解)
如图,求∠A+∠B+∠C+∠D+∠E+∠F 的度数(提示:构造四边形,利用多边形内角和求解)