题目内容
7.已知矩形ABCD中,AB=2BC,在CD上取一点E,使得∠EAB=30°,AE=AB,则∠EBC的度数为( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
分析 根据矩形的性质求出∠ABC=90°,根据等腰三角形的性质得出∠ABE=∠AEB,根据三角形内角和定理求出∠ABE,即可得出答案.
解答 解:
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵∠EAB=30°,AB=AE,
∴∠ABE=∠AEB=$\frac{1}{2}$(180°-∠EAB)=75°,
∴∠EBC=90°-75°=15°,
故选A.
点评 本题考查了矩形的性质,等腰三角形的性质,三角形内角和定理的应用,能求出∠ABE和∠ABC的度数是解此题的关键,注意:矩形的四个角都是直角,难度适中.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图,若点B与点A关于x轴对称,则点B的坐标是(1,-2).
如图,若点B与点A关于x轴对称,则点B的坐标是(1,-2).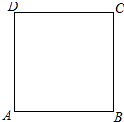 如图,在边长为1的正方形ABCD的边上有一个动点P,点P由点A(起点)沿着折线ABCD向点D(终点)移动,设点P移动的路程为x,△DAP的面积为S,求S与x的函数关系.
如图,在边长为1的正方形ABCD的边上有一个动点P,点P由点A(起点)沿着折线ABCD向点D(终点)移动,设点P移动的路程为x,△DAP的面积为S,求S与x的函数关系. 如图,求∠A+∠B+∠C+∠D+∠E+∠F 的度数(提示:构造四边形,利用多边形内角和求解)
如图,求∠A+∠B+∠C+∠D+∠E+∠F 的度数(提示:构造四边形,利用多边形内角和求解)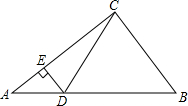 如图,在Rt△ABC中,∠ACB=90°,tanB=$\frac{4}{3}$,点D,E分别在边AB,AC上,DE⊥AC,DE=6,DB=20,则tan∠BCD的值是$\frac{8}{3}$.
如图,在Rt△ABC中,∠ACB=90°,tanB=$\frac{4}{3}$,点D,E分别在边AB,AC上,DE⊥AC,DE=6,DB=20,则tan∠BCD的值是$\frac{8}{3}$.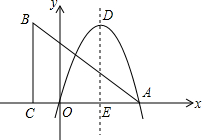 如图,在直角坐标系中,点A,C在x轴上,且AC=8,AB=10,∠ACB=90°
如图,在直角坐标系中,点A,C在x轴上,且AC=8,AB=10,∠ACB=90°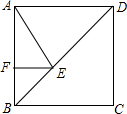 如图,正方形ABCD的边长为4+2$\sqrt{2}$,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长是2.
如图,正方形ABCD的边长为4+2$\sqrt{2}$,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长是2.