题目内容
5.已知二次函数y=(x-1)2-t2(t≠0),方程(x-1)2-t2-1=0的两根分别为m,n(m<n),方程(x-1)2-t2-2=0的两根分别为p,q(p<q),判断m,n,p,q的大小关系是p<m<n<q(用“<”连接)分析 画出二次函数y=(x-1)2-t2(t≠0)的图象,结合图象即可判断出m,n,p,q的大小.
解答  解:二次函数y=(x-1)2-t2(t≠0)的图象如右:
解:二次函数y=(x-1)2-t2(t≠0)的图象如右:
根据图可知p<m<n<q,
故答案为:p<m<n<q.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是画出二次函数y=(x-1)2-t2(t≠0)的图象,此题难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.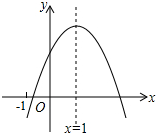 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )| A. | abc<0 | B. | 2a+b=0 | C. | b2-4ac>0 | D. | a-b+c>0 |
10.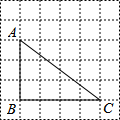 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA=( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA=( )
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA=( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则sinA=( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
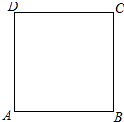 如图,在边长为1的正方形ABCD的边上有一个动点P,点P由点A(起点)沿着折线ABCD向点D(终点)移动,设点P移动的路程为x,△DAP的面积为S,求S与x的函数关系.
如图,在边长为1的正方形ABCD的边上有一个动点P,点P由点A(起点)沿着折线ABCD向点D(终点)移动,设点P移动的路程为x,△DAP的面积为S,求S与x的函数关系.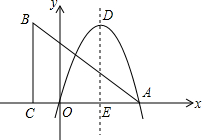 如图,在直角坐标系中,点A,C在x轴上,且AC=8,AB=10,∠ACB=90°
如图,在直角坐标系中,点A,C在x轴上,且AC=8,AB=10,∠ACB=90°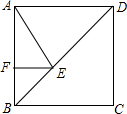 如图,正方形ABCD的边长为4+2$\sqrt{2}$,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长是2.
如图,正方形ABCD的边长为4+2$\sqrt{2}$,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长是2.