Question

19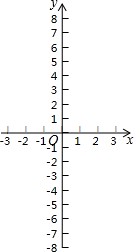．六个函数分别是①y=x；②y=-x+1；③y=x²；④y=-x²+2x-1；⑤y=x³；⑥y=-x³+1．
（1）其中一次函数是①，②，二次函数是③，④，则⑤，⑥的函数可以定义为三次函数；
（2）我们可以借鉴以前研究函数的经验，先探索函数y=x³的图象和性质；
①填写下表，画出函数的图象；
②观察图象，写出该函数两条不同类型的性质；

x	…	-2	-$\frac{3}{2}$	-1	0	1	$\frac{3}{2}$	2	…
y=x3	…								…

（3）若点A（a，b）（a＞0）是函数y=x³图象上一点，点A关于y轴的对称点为点B，点A关于原点O的对称点为点C，若顺次连接A，B，C，则△ABC的形状为直角三角形；
（4）函数y=-x³+1的图象关于点（0，1）成中心对称图形．

Answer 1

分析 （1）根据未知数的最高次数是3，即可判定是三次函数．
（2）①先列表后描点画图即可，②观察图象即可解决问题．
（3）根据如果三角形一边上的中线等于这边的一半，那么最高三角形是直角三角形．
（4）根据函数y=-x³+1的图象是由函数y=x³图象向上平移1个单位得到，由此即可解决问题．

解答 解：（1）⑤⑥是三次函数．
故答案为三次函数．
（2）①表格．图象如图1所示，


②y随x增大而增大，函数图象是中心对称图形．
（3）如图2所示，

∵函数y=x³图象是中心对称图形，
∵点A关于y轴的对称点为点B，点A关于原点O的对称点为点C
∴OA=OC=OB，O、A、C共线，
即OB=$\frac{1}{2}$AC，
∴△ABC是直角三角形．
故答案为直角三角形．
（4）函数y=-x³+1的图象是由函数y=x³图象向上平移1个单位得到，
∴函数y=-x³+1的图象的对称中心坐标为（0，1），
故答案为（0，1）．

点评 本题考查二次函数综合题、三次函数等知识，解题的关键是熟练掌握描点法画图，学会根据图象说出函数的性质，掌握图象平移个规律，属于中考压轴题，也是创新题目．