题目内容
6.下列命题中,是真命题的是( )①两条直线被第三条直线所截,同位角相等;
②在同一平面内,垂直于同一直线的两条直线互相平行
③三角形的三条高中,必有一条在三角形的内部
④$\sqrt{-2}$是一个负数.
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
分析 利用平行线的性质、算术平方根的定义、三角形的高的定义分别判断后即可确定正确的选项.
解答 解:①两条平行直线被第三条直线所截,同位角相等,故错误,是假命题;
②在同一平面内,垂直于同一直线的两条直线互相平行,正确,是真命题;
③三角形的三条高中,必有一条在三角形的内部,正确,是真命题;
④$\sqrt{-2}$无意义,不是负数,故错误,
故选B.
点评 本题考查了命题与定理的知识,解题的关键是了解平行线的性质、算术平方根的定义、三角形的高的定义,难度不大.

练习册系列答案
相关题目
16. 如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )
如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )
 如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )
如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )| A. | 4 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
14.能够判定一个四边形是菱形的条件是( )
| A. | 对角线互相垂直平分 | B. | 对角线互相平分且相等 | ||
| C. | 对角线相等且互相垂直 | D. | 对角线互相垂直 |
1. 如图,下列条件中,能判定DE∥AC的是( )
如图,下列条件中,能判定DE∥AC的是( )
 如图,下列条件中,能判定DE∥AC的是( )
如图,下列条件中,能判定DE∥AC的是( )| A. | ∠BED=∠EFC | B. | ∠1=∠2 | C. | ∠BEF+∠B=180° | D. | ∠3=∠4 |
15.下列多项式中,不能用平方差公式分解的是( )
| A. | -m4-n4 | B. | -16x2+y2 | C. | 1.96-x2 | D. | $\frac{1}{9}$a2-$\frac{1}{4}$b2 |

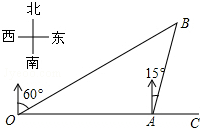 如图,港口A在观测站O的正东方向相距4km,某船从A出发,沿北偏东15°方向航行5分钟后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的速度(精确到整数位).参考数值:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.
如图,港口A在观测站O的正东方向相距4km,某船从A出发,沿北偏东15°方向航行5分钟后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的速度(精确到整数位).参考数值:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.