解方程:$\frac{x-2}{x+2}$-$\frac{x+2}{x-2}$=$\frac{16}{{x}^{2}-4}$．题目和参考答案——青夏教育精英家教网—

题目内容

3．解方程：$\frac{x-2}{x+2}$-$\frac{x+2}{x-2}$=$\frac{16}{{x}^{2}-4}$．

分析分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

解答解：方程两边同乘以（x+2）（x-2），得（x-2）²-（x+2）²=16，
解得：x=-2，
检验：当x=-2时，（x+2）（x-2）=0，
则x=-2是增根，原方程无解．

点评此题考查了解分式方程，利用了转化的思想，解分式方程时注意要检验．

练习册系列答案

相关题目

13．

如图，AB∥CD，∠A=45°，∠C=28°，则∠AEC的大小为（　　）

14．能够判定一个四边形是菱形的条件是（　　）

	A．	对角线互相垂直平分		B．	对角线互相平分且相等
	C．	对角线相等且互相垂直		D．	对角线互相垂直

11．居民区内的“广场舞”引起社会关注，小明想了解本小区居民对“广场舞”的看法，进行了一次抽样调查，把居民对“广场舞”的看法分为四个层次：A．非常赞同；B．赞同但要有时间限制；C．无所谓；D．不赞同．并将调查结果绘制了图1和图2两幅不完整的统计图．请你根据图中提供信息回答下列问题：
（1）求本次被抽查的居民有多少人？
（2）将图1和图2补充完整；
（3）求图2中“C”层次所在扇形的圆心角的度数；
（4）估计该小区4000名居民中对“广场舞”的看法表示赞同（包括A层次和B层次）的大约有多少人．

18．若x，y满足方程组$\left\{\begin{array}{l}{x+y=4}\\{x-2y=1}\end{array}\right.$，则代数式4x²-4xy+y²的值为25．

8．解方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$时，某同学把c看错后得到$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$，而正确的解是$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$，那么a、b、c的值是（　　）

	A．	a=4，b=5，c=2		B．	a，b，c的值不能确定
	C．	a=4，b=5，c=-2		D．	a，b不能确定，c=-2

15．下列多项式中，不能用平方差公式分解的是（　　）

-m⁴-n⁴

$\frac{1}{9}$a²-$\frac{1}{4}$b²

12．

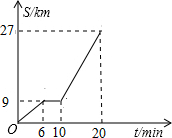如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s（km）与时间t（分钟）的函数关系图，观察图中所提供的信息，解答下列问题：
（1）汽车在前6分钟内的平均速度是90千米/小时，汽车在兴国服务区停了多长时间？4分钟；
（2）当10≤t≤20时，求S与t的函数关系式；
（3）规定：高速公路时速超过120千米/小时为超速行驶，试判断当10≤t≤20时，该汽车是否超速，说明理由．

13．若不等式组$\left\{\begin{array}{l}{x+a≥0}\\{1-2x＞x-2}\end{array}\right.$有三个整数解，则实数a的取值范围是（　　）

试题分类