题目内容
2.国家要求中小学生每天锻炼1小时,某校开展了形式多样的“阳光体育运动”活动,小明本班同学参加锻炼的情况进行了统计,并绘制了图1和图2.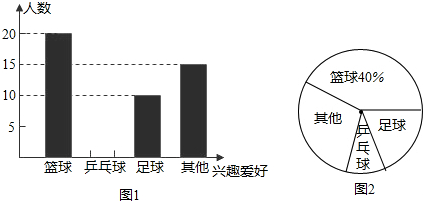
(1)求被调查班级的学生人数.
(2)求喜欢“乒乓球”的学生人数.并在图1中将“乒乓球”部分的图形补充完整.
(3)若该校共有2000名学生,请估计喜欢“足球”的学生人数.
分析 (1)根据喜欢篮球的有20人,占40%,据此即可求得总人数;
(2)利用总人数减去其它各项的人数,求得喜欢乒乓球的人数,即可补全直方图;
(3)利用总人数2000乘以对应的比例即可求得.
解答 解:(1)被调查班级的学生人数为20÷40%=50(人);
(2)喜欢“乒乓球”的学生人数为50-20-10-15=5(人),补全图形如下:
(3)$\frac{10}{50}$×2000=400(人),
答:估计喜欢“足球”的学生人数为400.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
13. 如图,AB∥CD,∠A=45°,∠C=28°,则∠AEC的大小为( )
如图,AB∥CD,∠A=45°,∠C=28°,则∠AEC的大小为( )
 如图,AB∥CD,∠A=45°,∠C=28°,则∠AEC的大小为( )
如图,AB∥CD,∠A=45°,∠C=28°,则∠AEC的大小为( )| A. | 17° | B. | 28° | C. | 45° | D. | 73° |
7.在△ABC中,∠C=90°,∠A=30°,若CD是高,且CD=1,则a,b,c三边的长分别是( )
| A. | a=$\sqrt{3}$,b=2,c=$\sqrt{7}$ | B. | a=2,b=$\frac{2\sqrt{3}}{3}$,c=$\frac{4\sqrt{3}}{3}$ | C. | a=$\frac{2\sqrt{3}}{3}$,b=2,c=$\frac{4\sqrt{3}}{3}$ | D. | a=2,b=2,c=4 |
14.能够判定一个四边形是菱形的条件是( )
| A. | 对角线互相垂直平分 | B. | 对角线互相平分且相等 | ||
| C. | 对角线相等且互相垂直 | D. | 对角线互相垂直 |


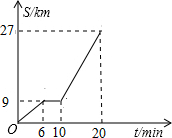 如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s(km)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列问题:
如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s(km)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列问题: