题目内容
13. 如图,在平面直角坐标系中,已知A(-5,0),B(5,0),C(3,6),则△ABC重心的坐标是( )
如图,在平面直角坐标系中,已知A(-5,0),B(5,0),C(3,6),则△ABC重心的坐标是( )| A. | ($\frac{1}{3}$,1) | B. | ($\frac{2}{3}$,1) | C. | (1,$\frac{2}{3}$) | D. | (1,2) |
分析 根据三角形的重心的概念作出重心,根据重心的性质得到OG=$\frac{1}{3}$OC,根据平行线分线段成比例定理计算即可.
解答 解: ∵A(-5,0),B(5,0),
∵A(-5,0),B(5,0),
∴点O是AB的中点,
连接OC,作中线AH交OC于G,则点G是△ABC的重心,
∴OG=$\frac{1}{3}$OC,
作GE⊥AB于E,CF⊥AB于F,
则GE∥CF,
∴$\frac{OE}{OF}$=$\frac{GE}{CF}$=$\frac{OG}{OC}$=$\frac{1}{3}$,
∴OE=1,GE=2,
∴△ABC重心的坐标是(1,2),
故选:D.
点评 本题考查的是三角形的重心的概念和性质、坐标与图形性质,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.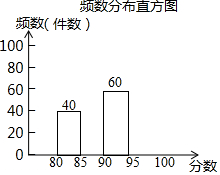 某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动,全县有1000名学生的作品(每人1件作品)参加了这个评比活动,评比的方法是给每件作品一个分值,最高分100分,最低分80分.现从这1000件作品中随机抽取了m件作品,并把这m件作品的分值制成了如下频数分布表和频数分布直方图:
某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动,全县有1000名学生的作品(每人1件作品)参加了这个评比活动,评比的方法是给每件作品一个分值,最高分100分,最低分80分.现从这1000件作品中随机抽取了m件作品,并把这m件作品的分值制成了如下频数分布表和频数分布直方图:
(1)求出m的值;
(2)补全频数分布表和频数分布直方图;
(3)如果作品的分值在95分(含95分)以上的可以获得一等奖,试估计全县参加此项活动获得一等奖的人数.
 某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动,全县有1000名学生的作品(每人1件作品)参加了这个评比活动,评比的方法是给每件作品一个分值,最高分100分,最低分80分.现从这1000件作品中随机抽取了m件作品,并把这m件作品的分值制成了如下频数分布表和频数分布直方图:
某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动,全县有1000名学生的作品(每人1件作品)参加了这个评比活动,评比的方法是给每件作品一个分值,最高分100分,最低分80分.现从这1000件作品中随机抽取了m件作品,并把这m件作品的分值制成了如下频数分布表和频数分布直方图:| 分数段 | 频数 | 百分比 |
| 80≤x<85 | 40 | 20% |
| 85≤x<90 | 80 | 40% |
| 90≤x<95 | 60 | 30% |
| 95≤x<100 | 20 | 10% |
(2)补全频数分布表和频数分布直方图;
(3)如果作品的分值在95分(含95分)以上的可以获得一等奖,试估计全县参加此项活动获得一等奖的人数.
2. 如图,某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1 000名学生中,随机抽取了若干名学生进行调查,了解学生最喜欢的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
如图,某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1 000名学生中,随机抽取了若干名学生进行调查,了解学生最喜欢的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
解答下列问题:
(1)本次调查中的样本容量是120;
(2)求出a与b的值.
(3)试估计上述1 000名学生中最喜欢羽毛球运动的人数.
 如图,某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1 000名学生中,随机抽取了若干名学生进行调查,了解学生最喜欢的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
如图,某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1 000名学生中,随机抽取了若干名学生进行调查,了解学生最喜欢的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:| 球类名称 | 乒乓球 | 排球 | 羽毛球 | 足球 | 篮球 |
| 人数 | a | 12 | 36 | 16 | b |
(1)本次调查中的样本容量是120;
(2)求出a与b的值.
(3)试估计上述1 000名学生中最喜欢羽毛球运动的人数.
 如图,过等腰直角三角板ABC顶点C作AB边的平行线CD,再作∠BCD的平分线CE,则∠BCE=22.5°.
如图,过等腰直角三角板ABC顶点C作AB边的平行线CD,再作∠BCD的平分线CE,则∠BCE=22.5°.