题目内容
13.已知矩形ABCD的一条边长为5,对角线AC、BD相交于点O,若AO、CO的长是关于x的方程x2+2(m-1)x+m2+11=0的两个根,则矩形的面积为5$\sqrt{11}$.分析 由矩形的性质可知:AO=CO,即x的方程x2+2(m-1)x+m2+11=0的两根相等,所以△=0,即可把m的值求出,利用勾股定理可求出矩形的另外一边长,再利用矩形的面积计算即可
解答 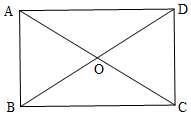 解:如图,∵四边形ABCD是矩形,
解:如图,∵四边形ABCD是矩形,
∴AO=CO,∠A=90°,
∵AO、CO的长是关于x的方程x2+2(m-1)x+m2+11=0的两个根,
∴△=[2(m-1)]2-4×1×(m2+11)=0,
4(m2-2m+1)-4m2-44=0,
-8m+4-44=0,
m=-5,
则原方程为:x2-12x+36=0,
(x-6)2=0,
x1=x2=6,
∴AO=CO=6,
在Rt△ABD中,由勾股定理得:AD=$\sqrt{{6}^{2}-{5}^{2}}$=$\sqrt{11}$,
∴S矩形ABCD=AB×AD=5$\sqrt{11}$,
故答案为:5$\sqrt{11}$.
点评 本题考查了矩形的性质、根的判别式的运用以及勾股定理、解一元二次方程的方法、矩形的面积公式的运用,题目的综合性很强,难度中等.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
8.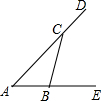 如图,B、C两点在线段AE、AD上,若在线段BC上求一点P,使点P到AD,AE的距离相等,则P点是( )
如图,B、C两点在线段AE、AD上,若在线段BC上求一点P,使点P到AD,AE的距离相等,则P点是( )
 如图,B、C两点在线段AE、AD上,若在线段BC上求一点P,使点P到AD,AE的距离相等,则P点是( )
如图,B、C两点在线段AE、AD上,若在线段BC上求一点P,使点P到AD,AE的距离相等,则P点是( )| A. | 线段BC的中点 | B. | AE的垂直平分线与线段BC的交点 | ||
| C. | AC的垂直平分线与线段BC的交点 | D. | ∠CAB的平分线与BC的交点 |
 如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为18m.设AD的长为x m,菜园ABCD的面积为y m2.则函数y关于自变量x的函数关系式是y=(30-2x)x,x的取值范围是6≤x<15.
如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为18m.设AD的长为x m,菜园ABCD的面积为y m2.则函数y关于自变量x的函数关系式是y=(30-2x)x,x的取值范围是6≤x<15.
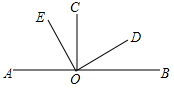 如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1-∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角)
如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1-∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角)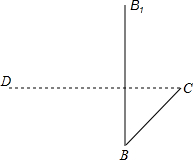 (1)用斜二测画法补全长方体ABCD-A1B1C1D1 (不必写画法);
(1)用斜二测画法补全长方体ABCD-A1B1C1D1 (不必写画法);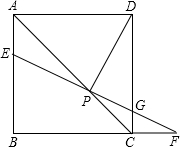 已知:如图,点P是正方形ABCD的对角线AC上一点,过点P作EF⊥DP,交AB于点E,交CD于点G,交BC的延长线于点F.
已知:如图,点P是正方形ABCD的对角线AC上一点,过点P作EF⊥DP,交AB于点E,交CD于点G,交BC的延长线于点F.