题目内容
 如图,在半径为2,圆心角为90°的扇形ACB内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为
如图,在半径为2,圆心角为90°的扇形ACB内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为考点:扇形面积的计算
专题:
分析:根据BC为直径可知∠CDB=90°,在等腰直角三角形ABC中,CD垂直平分AB,CD=DB,D为半圆的中点,阴影部分的面积可以看作是扇形ACB的面积与△ADC的面积之差.
解答:解:在Rt△ACB中,
∵AC=BC=2,
∴AB=
=2
,
∵BC是半圆的直径,
∴∠CDB=90°,
在等腰Rt△ACB中,
∵CD垂直平分AB,CD=BD=
,
∴D为半圆的中点,
S阴影部分=S扇形ACB-S△ADC=
π×22-
×(
)2=π-1.
故答案为:π-1.
∵AC=BC=2,
∴AB=
| 22+22 |
| 2 |
∵BC是半圆的直径,
∴∠CDB=90°,
在等腰Rt△ACB中,
∵CD垂直平分AB,CD=BD=
| 2 |
∴D为半圆的中点,
S阴影部分=S扇形ACB-S△ADC=
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
故答案为:π-1.
点评:本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
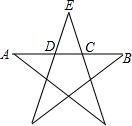 如图,在五角星图形中,AD=BC,C,D两点都是AB的黄金分割点,AB=1,求CD的长.
如图,在五角星图形中,AD=BC,C,D两点都是AB的黄金分割点,AB=1,求CD的长. 如图,将甲图经过
如图,将甲图经过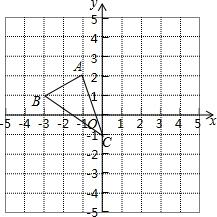 在直角坐标系中,△ABC的顶点坐标是A(-1,2)、B(-3,1)、C(0,-1).
在直角坐标系中,△ABC的顶点坐标是A(-1,2)、B(-3,1)、C(0,-1).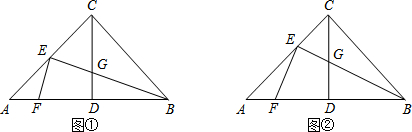
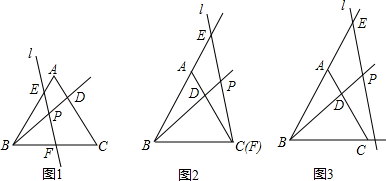
 DE为△ABC的中位线,连接BE,且BE=BC,延长DE到点F,使EF=BE,连接CF,BF.
DE为△ABC的中位线,连接BE,且BE=BC,延长DE到点F,使EF=BE,连接CF,BF. 如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,反比例函数y=
如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,反比例函数y=