题目内容
 如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,反比例函数y=
如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,反比例函数y=| m |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:根据一次函数y=kx-2的解析式可直接算出E点坐标,根据平行线分线段成比例定理可得
=
,再代入相应线段长可算出CO的长,进而得到点C的坐标,把点C的坐标代入y=kx-2中即可得到一次函数的解析式;然后再算出A点的坐标,把A点的坐标(6,1)代入y=
得反比例函数的解析式,根据等腰三角形的对称性求得P的坐标,然后根据待定系数法求得直线PA,联立方程解方程即可求得M的坐标.
| AB |
| OE |
| BC |
| OC |
| m |
| x |
解答:解:∵一次函数的解析式为y=kx-2,
∴当x=0时,y=k×0-2=-2,
∴点E的坐标为(0,-2);
∵AB∥EO,
∴
=
,
即
=
,
∴OC=4,
∴点C的坐标为(4,0),
把点C的坐标(4,0)代入y=kx-2,得k=
,
∴一次函数的解析式为y=
x-2,
∵BC=2,
∴A点的坐标为(6,1),
∵反比例函数y=
的图象经过点A,
∴m=6,
∴反比例函数y=
,
∵AP=AE,
∴AP、AE关于直线AD对称,
∵AB=1,
∴直线AD为y=1,
∴P(0,4)
设直线AP的解析式为y=ax+4,
∵A点的坐标为(6,1),
∴6a+4=1,解得a=-
,
∴直线AP的解析式为y=-
x+4,
解
得
或
,
∴M点的坐标为(2,3).
∴当x=0时,y=k×0-2=-2,
∴点E的坐标为(0,-2);
∵AB∥EO,
∴
| AB |
| OE |
| BC |
| OC |
即
| 1 |
| 2 |
| 2 |
| OC |
∴OC=4,
∴点C的坐标为(4,0),
把点C的坐标(4,0)代入y=kx-2,得k=
| 1 |
| 2 |
∴一次函数的解析式为y=
| 1 |
| 2 |
∵BC=2,
∴A点的坐标为(6,1),
∵反比例函数y=
| m |
| x |
∴m=6,
∴反比例函数y=
| 6 |
| x |
∵AP=AE,
∴AP、AE关于直线AD对称,
∵AB=1,
∴直线AD为y=1,
∴P(0,4)
设直线AP的解析式为y=ax+4,
∵A点的坐标为(6,1),
∴6a+4=1,解得a=-
| 1 |
| 2 |
∴直线AP的解析式为y=-
| 1 |
| 2 |
解
|
|
|
∴M点的坐标为(2,3).
点评:此题主要考查了待定系数法求一次函数解析式与反比例函数解析式,以及平行线分线段成比例定理,解决问题的关键是算出OC的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果a=b,那么下列结论中不一定成立的是( )
A、
| ||
| B、a-b=0 | ||
| C、2a=a+b | ||
| D、a2=ab |
已知
=
,则( )
| a |
| b |
| 2 |
| 3 |
| A、2a=3b | ||||
B、
| ||||
C、
| ||||
D、
|
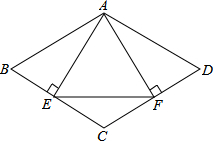 如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则的△AEF的面积是( )
如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则的△AEF的面积是( )A、4
| ||
B、3
| ||
C、2
| ||
D、
|
 如图,在一长方形内有对角线长分别为2,3的菱形以及半径为1的圆,若一点随机落在这两个图形内,则概率较大的是( )
如图,在一长方形内有对角线长分别为2,3的菱形以及半径为1的圆,若一点随机落在这两个图形内,则概率较大的是( )| A、落在菱形内 | B、落在圆内 |
| C、无法判断 | D、一样大 |
 如图,在半径为2,圆心角为90°的扇形ACB内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为
如图,在半径为2,圆心角为90°的扇形ACB内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为